题目内容
19.腰长为20cm,且底角为15°的等腰三角形,其腰上的高等于10cm.分析 根据等腰三角形的性质可求得两底角的度数,从而可求得顶角的邻补角的度数为30°,根据直角三角形中30度的角所对的边是斜边的一半即可求得腰上的高的长.
解答  解:如图,AB=AC=20cm,∠ABC=∠ACB=15°,过C作CD⊥AB,交BA延长线于D,
解:如图,AB=AC=20cm,∠ABC=∠ACB=15°,过C作CD⊥AB,交BA延长线于D,
∵∠B=15°,AB=AC,
∴∠DAC=30°,
∵CD为AB上的高,AC=20cm,
∴CD=$\frac{1}{2}$AC=10cm.
故答案为:10.
点评 此题主要考查含30度角的直角三角形的性质和等腰三角形的性质,三角形外角性质的应用,注意:在直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
相关题目
4.下列各式计算正确的是( )
| A. | 2$\sqrt{3}$×3$\sqrt{3}$=6$\sqrt{3}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | 5$\sqrt{3}$-2$\sqrt{2}$=3$\sqrt{3}$ | D. | $\sqrt{2}$÷$\sqrt{3}$=$\frac{\sqrt{6}}{3}$ |
9.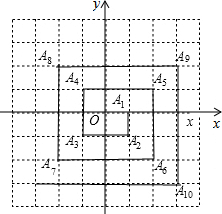 如图,已知A1(1,0),A2(1,1),A3(-1,-1),A4(-1,1),A5(2,1),…则点A2010的坐标是( )
如图,已知A1(1,0),A2(1,1),A3(-1,-1),A4(-1,1),A5(2,1),…则点A2010的坐标是( )
 如图,已知A1(1,0),A2(1,1),A3(-1,-1),A4(-1,1),A5(2,1),…则点A2010的坐标是( )
如图,已知A1(1,0),A2(1,1),A3(-1,-1),A4(-1,1),A5(2,1),…则点A2010的坐标是( )| A. | (502,502) | B. | (-501,-501) | C. | (503,-503) | D. | (-501,501) |
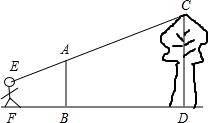 如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=2.5m,人高EF=1.5m,求树高CD.
如图,直立在B处的标杆AB=2.4m,直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上(点F,B,D也在同一条直线上).已知BD=8m,FB=2.5m,人高EF=1.5m,求树高CD. 如图,在△ABC中,点E在BC上,CD⊥AB,EF⊥AB,垂足分别为D、F.
如图,在△ABC中,点E在BC上,CD⊥AB,EF⊥AB,垂足分别为D、F.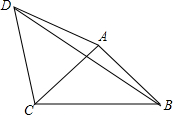 如图,四边形ABCD中,AD=3,CD=4,∠ABC=∠ACB=∠ADC=45°,则BD的长为$\sqrt{34}$.
如图,四边形ABCD中,AD=3,CD=4,∠ABC=∠ACB=∠ADC=45°,则BD的长为$\sqrt{34}$.