题目内容
17.如图,是一组按照某种程度摆放成的图案,则图6中三角形的个数是( )
| A. | 18 | B. | 19 | C. | 20 | D. | 21 |
分析 由图可知:第一个图案有三角形1个,第二图案有三角形1+3=4个,第三个图案有三角形1+3+4=8个,第四个图案有三角形1+3+4+4=12,…第n个图案有三角形4(n-1)个,由此得出规律解决问题.
解答 解:第一个图案有三角形1个,
第二图案有三角形1+3=4个,
第三个图案有三角形1+3+4=8个,
第四个图案有三角形1+3+4+4=12,
第五个图案有三角形1+3+4+4+4=16,
第六个图案有三角形1+3+4+4+4+4=20.
故选C.
点评 此题主要考查了图形的变化规律,注意由特殊到一般的分析方法.这类题型在中考中经常出现.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
8.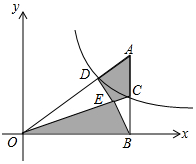 如图,点C在反比例函数y=$\frac{1}{x}$(x>0)的图象上,CB⊥x轴于点B,延长BC至A,使得AC=BC,连接AO交反比例函数的图象于点D,连接BD,OC交于点E,随着点C的横坐标的增大,图中阴影部分面积S1+S2的大小变化情况是( )
如图,点C在反比例函数y=$\frac{1}{x}$(x>0)的图象上,CB⊥x轴于点B,延长BC至A,使得AC=BC,连接AO交反比例函数的图象于点D,连接BD,OC交于点E,随着点C的横坐标的增大,图中阴影部分面积S1+S2的大小变化情况是( )
 如图,点C在反比例函数y=$\frac{1}{x}$(x>0)的图象上,CB⊥x轴于点B,延长BC至A,使得AC=BC,连接AO交反比例函数的图象于点D,连接BD,OC交于点E,随着点C的横坐标的增大,图中阴影部分面积S1+S2的大小变化情况是( )
如图,点C在反比例函数y=$\frac{1}{x}$(x>0)的图象上,CB⊥x轴于点B,延长BC至A,使得AC=BC,连接AO交反比例函数的图象于点D,连接BD,OC交于点E,随着点C的横坐标的增大,图中阴影部分面积S1+S2的大小变化情况是( )| A. | 一直减小 | B. | 一直不变 | C. | 先减小后增大 | D. | 先增大后减小 |
2.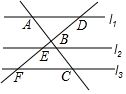 如图,已知l1∥l2∥l3,直线AC、DF分别交直线l1、l2、l3于点A、B、C,和点D、E、F,若DE=2,DF=3,则下列结论中,错误的是( )
如图,已知l1∥l2∥l3,直线AC、DF分别交直线l1、l2、l3于点A、B、C,和点D、E、F,若DE=2,DF=3,则下列结论中,错误的是( )
 如图,已知l1∥l2∥l3,直线AC、DF分别交直线l1、l2、l3于点A、B、C,和点D、E、F,若DE=2,DF=3,则下列结论中,错误的是( )
如图,已知l1∥l2∥l3,直线AC、DF分别交直线l1、l2、l3于点A、B、C,和点D、E、F,若DE=2,DF=3,则下列结论中,错误的是( )| A. | $\frac{AD}{CF}$=$\frac{2}{3}$ | B. | $\frac{BC}{AB}$=$\frac{1}{2}$ | C. | $\frac{AB}{AC}$=$\frac{2}{3}$ | D. | $\frac{EF}{DF}$=$\frac{1}{3}$ |
9.下列说法中错误的是( )
| A. | $\frac{1}{2}$是0.25的一个平方根 | B. | 正数a的两个平方根的和为0 | ||
| C. | $\frac{9}{16}$的平方根是$\frac{3}{4}$ | D. | 当x≠0时,-x2没有平方根 |
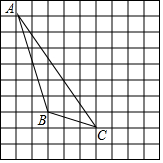 如图,每个小正方形的边长均为1,每个小方格的顶点叫格点.
如图,每个小正方形的边长均为1,每个小方格的顶点叫格点.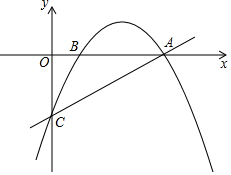 如图,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.
如图,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.