题目内容
16.若二次根式$\frac{\sqrt{x-2}}{x-4}$有意义,则x的取值范围是x≥2,且x≠4;若分式$\frac{|x|-1}{x-1}$的值为零,则x的值等于-1.分析 根据二次根式有意义的条件可得x-2≥0,根据分式有意义的条件可得x-4≠0,再解即可;根据分式值为零的条件可得:|x|-1=0且x-1≠0,再解即可.
解答 解:由题意得:x-2≥0,且x-4≠0,
解得:x≥2,且x≠4;
由题意得:|x|-1=0且x-1≠0,
解得:x=-1,
故答案为:x≥2,且x≠4;-1.
点评 此题主要考查了二次根式有意义和分式有意义的条件,以及分式值为零的条件,关键是掌握二次根式中的被开方数是非负数,分式有意义的条件是分母不等于零;分式值为零的条件是分子等于零且分母不等于零.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
6. 如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,随机将方格内容白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的概率是( )
如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,随机将方格内容白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的概率是( )
 如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,随机将方格内容白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的概率是( )
如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,随机将方格内容白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{2}{9}$ |
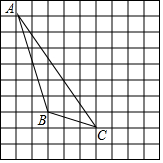 如图,每个小正方形的边长均为1,每个小方格的顶点叫格点.
如图,每个小正方形的边长均为1,每个小方格的顶点叫格点.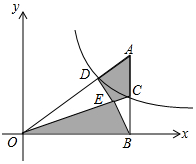 如图,点C在反比例函数y=$\frac{1}{x}$(x>0)的图象上,CB⊥x轴于点B,延长BC至A,使得AC=BC,连接AO交反比例函数的图象于点D,连接BD,OC交于点E,随着点C的横坐标的增大,图中阴影部分面积S1+S2的大小变化情况是( )
如图,点C在反比例函数y=$\frac{1}{x}$(x>0)的图象上,CB⊥x轴于点B,延长BC至A,使得AC=BC,连接AO交反比例函数的图象于点D,连接BD,OC交于点E,随着点C的横坐标的增大,图中阴影部分面积S1+S2的大小变化情况是( )