题目内容
9.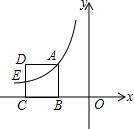 如图,正方形ABCD的边BC在x轴的负半轴上,其中E是CD的中点,函数y=$\frac{k}{x}$的图象经过点A、E.若B点的坐标是(-3,0),则k的值为( )
如图,正方形ABCD的边BC在x轴的负半轴上,其中E是CD的中点,函数y=$\frac{k}{x}$的图象经过点A、E.若B点的坐标是(-3,0),则k的值为( )| A. | -5 | B. | -4 | C. | -6 | D. | -9 |
分析 根据正方形的性质,设出A(-3,n),则E(-3-n,$\frac{1}{2}$n)代入反比例函数解析式,得出k=-3×n=(-3-n)•$\frac{1}{2}$n,求得n=3,进而就可求得k的值.
解答 解:∵B点的坐标是(-3,0),四边形ABCD是正方形,
设A(-3,n),
∴E(-3-n,$\frac{1}{2}$n),
∵函数y=$\frac{k}{x}$的图象经过点A、E.,
则-3×n=(-3-n)•$\frac{1}{2}$n,
∴n=3,
∴k=-3×3=-9.
故选D.
点评 本题考查了反比例函数图象上点的坐标特征和正方形的性质,要知道,所有在反比例函数上的点的横纵坐标的积应等于比例系数.

练习册系列答案
相关题目
19.下列计算正确的是( )
| A. | a3-a2=a | B. | a3•a2=a6 | C. | a3÷a2=a | D. | (a3)2=a5 |
14.若am=2,an=3,则am-n等于( )
| A. | 5 | B. | 6 | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
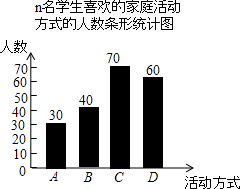 在“世界家庭日”前夕,某校团委随机抽取了n名本校学生,对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查.问卷中的家庭活动方式包括:
在“世界家庭日”前夕,某校团委随机抽取了n名本校学生,对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查.问卷中的家庭活动方式包括:
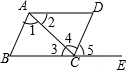 分别根据已知条件进行推理,得出结论,并说明理由.
分别根据已知条件进行推理,得出结论,并说明理由.