题目内容
12.在围棋盒中有x颗白棋和y颗黑棋,从盒中任意抽取一颗棋子,取得白色棋子的概率是$\frac{2}{5}$,如果再往盒中放进6颗黑色棋子,取得白棋子的概率是$\frac{1}{4}$,则原来盒中有白色棋子多少颗.分析 根据概率公式即可得方程组:$\left\{\begin{array}{l}{\frac{x}{x+y}=\frac{2}{5}}\\{\frac{x}{x+y+6}=\frac{1}{4}}\end{array}\right.$,解此方程组即可求得答案.
解答 解:根据题意得:
$\left\{\begin{array}{l}{\frac{x}{x+y}=\frac{2}{5}}\\{\frac{x}{x+y+6}=\frac{1}{4}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=6}\end{array}\right.$,
∴原来盒中有白色棋子4颗.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
2.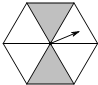 如图,一个正六边形转盘被分成6个全等三角形,任意转动这个转盘1次,当转盘停止时,指针指向阴影区域的概率是( )
如图,一个正六边形转盘被分成6个全等三角形,任意转动这个转盘1次,当转盘停止时,指针指向阴影区域的概率是( )
 如图,一个正六边形转盘被分成6个全等三角形,任意转动这个转盘1次,当转盘停止时,指针指向阴影区域的概率是( )
如图,一个正六边形转盘被分成6个全等三角形,任意转动这个转盘1次,当转盘停止时,指针指向阴影区域的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
3.下列各式中,是最简二次根式的是( )
| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{4a}$ | C. | $\sqrt{\frac{1}{5}}$ | D. | $\sqrt{{a}^{4}}$ |
 △ABC中,∠BAC=70°,BC=12,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,求:∠EAN的度数.
△ABC中,∠BAC=70°,BC=12,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,求:∠EAN的度数.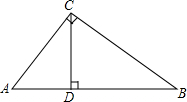 如图所示,AC⊥BC,CD⊥AB,AC=5cm,BC=12cm,AB=13cm,则点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.
如图所示,AC⊥BC,CD⊥AB,AC=5cm,BC=12cm,AB=13cm,则点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.