题目内容
7.四边形ABCD满足AB=CD,AC=BD,试通过画图来探究,四边形ABCD会是怎样的形状?分析 四边形ABCD是等腰梯形,画出图形,利用三角形全等的判定与等腰三角形的性质解决问题即可.
解答 解:四边形ABCD是等腰梯形.
如图,
假定AC与BD交于O点,
在△ABC和△DCB中
$\left\{\begin{array}{l}{AB=CD}\\{AC=BD}\\{BC=BC}\end{array}\right.$,
∴△ABC≌△DCB,
∴∠DBC=∠ACB,∠DCB=∠ABC,
∴OB=OC,∠DBA=∠ACD
又∵AC=BD,
∴OA=OD,∠CAD=∠BDA,
即△OAD和△OCD是两个顶角是对顶角的等腰三角形
所以∠DBA=∠ACB=∠CAD=∠BDA,
∵∠DBC=∠BDA,
∴AD平行BC,AB不平行于CD,
所以四边形ABCD是梯形
又∵AB=CD,
∴四边形ABCD为等腰梯形(两腰相等的梯形是等腰梯形).
点评 此题考查等腰梯形的判定,三角形全等的判定与性质,平行线的判定与性质,等腰三角形的判定与性质,结合图形灵活解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.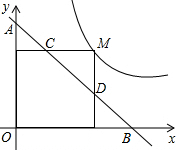 如图,M为双曲线y=$\frac{{\sqrt{3}}}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为( )
如图,M为双曲线y=$\frac{{\sqrt{3}}}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为( )
 如图,M为双曲线y=$\frac{{\sqrt{3}}}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为( )
如图,M为双曲线y=$\frac{{\sqrt{3}}}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为( )| A. | $2\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $2\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
16.下列方程的两个根互为倒数的是( )
| A. | x2-x-1=0 | B. | x2+x-1=0 | C. | 2x2+3x+1=0 | D. | 2x2-5x+2=0 |
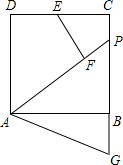 如图,P为正方形ABCD边BC上一点,F在AP上,且AF=AD,EF⊥AP交CD于点E,G为CB延长线上一点,BG=DE.
如图,P为正方形ABCD边BC上一点,F在AP上,且AF=AD,EF⊥AP交CD于点E,G为CB延长线上一点,BG=DE.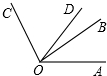 如图,∠BOC=2∠AOB,OD平分∠AOC,∠BOD=25°,求∠AOB的度数.
如图,∠BOC=2∠AOB,OD平分∠AOC,∠BOD=25°,求∠AOB的度数.