题目内容
7.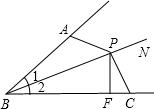 已知:如图,∠1=∠2,P为BN上的一点,PF⊥BC于F,PA=PC,
已知:如图,∠1=∠2,P为BN上的一点,PF⊥BC于F,PA=PC,(1)求证:∠PCB+∠BAP=180°;
(2)线段BF、线段BC、线段AB之间有何数量关系?写出你的猜想及证明思路.
分析 (1)过P点作PE⊥BA于点E,由∠1=∠2利用角平分线的性质即可得出PE=PF,结合PA=PC即可利用全等三角形的判定定理HL证出Rt△PAE≌Rt△PCF,由此可得出∠PCF=∠PAE,再根据邻补角互补可得出∠PAE+∠BAP=180°,将∠PAE替换成∠PCB即可证出结论;
(2)由Rt△PAE≌Rt△PCF可得出AE=CF,结合PB=PB即可证出Rt△PBE≌Rt△PBF,进而得出BE=BF,再根据边与边之间的关系即可得出2BF=AB+AC.
解答 (1)证明:过P点作PE⊥BA于点E,如图所示.
∵∠1=∠2,PF⊥BC,
∴PE=PF.
在Rt△PAE与Rt△PCF中,$\left\{\begin{array}{l}{PA=PC}\\{PE=PF}\end{array}\right.$,
∴Rt△PAE≌Rt△PCF(HL),
∴∠PCF=∠PAE.
∵∠PAE+∠BAP=180°,
∴∠PCB+∠BAP=180°.
(2)解:2BF=AB+BC.
证明:∵Rt△PAE≌Rt△PCF,
∴AE=CF.
在Rt△PBE和Rt△PBF中,$\left\{\begin{array}{l}{PB=PB}\\{PE=PF}\end{array}\right.$,
∴Rt△PBE≌Rt△PBF(HL),
∴BE=BF.
∴2BF=BE+BF=AB+AE+BF=AB+FC+BF=AB+AC.
点评 本题考查了全等三角形的判定于性质、角平分线的性质以及邻补角,解题的关键是:(1)利用HL证明Rt△PAE≌Rt△PCF;(2)利用HL证明Rt△PBE≌Rt△PBF.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15. 如图所示,AC⊥BC,AD⊥CD,AB=m,CD=n,则AC与m,n的大小关系是( )
如图所示,AC⊥BC,AD⊥CD,AB=m,CD=n,则AC与m,n的大小关系是( )
 如图所示,AC⊥BC,AD⊥CD,AB=m,CD=n,则AC与m,n的大小关系是( )
如图所示,AC⊥BC,AD⊥CD,AB=m,CD=n,则AC与m,n的大小关系是( )| A. | AC大于n | B. | AC小于m | C. | AC大于n且小于m | D. | 无法确定 |
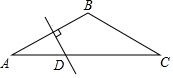 如图,在△ABC中,已知AB=BC,∠B=120°,AB的垂直平分线交AC于点D,若AC=6,求AD的长.
如图,在△ABC中,已知AB=BC,∠B=120°,AB的垂直平分线交AC于点D,若AC=6,求AD的长. 如图,△ABC内接于⊙O,∠ABC=71°,∠CAB=53°,点D在$\widehat{AC}$上,则∠ADB的大小为56度.
如图,△ABC内接于⊙O,∠ABC=71°,∠CAB=53°,点D在$\widehat{AC}$上,则∠ADB的大小为56度.