题目内容
19.已知a,b,c满足等式:3$\sqrt{a-b}$+4$\sqrt{c}$=16(a≥b,c≥0),且x=4$\sqrt{a-b}$-3$\sqrt{c}$,求x的取值范围.分析 设$\sqrt{a-b}$=m,$\sqrt{c}$=n,则3$\sqrt{a-b}$+4$\sqrt{c}$=16,则3m+4n=16,x=4$\sqrt{a-b}$-3$\sqrt{c}$即4m-3n=x,据此即可得到一个关于m和n的方程组,然后根据m和n是非负数求得x的范围.
解答 解:设$\sqrt{a-b}$=m,$\sqrt{c}$=n,
则3$\sqrt{a-b}$+4$\sqrt{c}$=16,则3m+4n=16,
x=4$\sqrt{a-b}$-3$\sqrt{c}$即4m-3n=x,
根据题意得$\left\{\begin{array}{l}{3m+4n=16}\\{4m-3n=x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=\frac{4x-48}{7}}\\{n=\frac{64-3x}{25}}\end{array}\right.$,
根据题意得$\left\{\begin{array}{l}{\frac{4x-48}{7}≥0}\\{\frac{64-3x}{25}≥0}\end{array}\right.$,
解得:12≤x≤$\frac{64}{3}$.
点评 本题考查了二次根式的化简,以及方程组和不等式组的解法,正确转化为关于m和n的方程组是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10. 小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )
小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )
 小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )
小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$+1 |
4.把4:9的前项加上8,要使比值不变,后项应加上( )
| A. | 27 | B. | 36 | C. | 18 | D. | 9 |
11.下列性质中,矩形具有但菱形不一定具有的是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | C. | 对角线相等 | D. | 对边平行 |
8.平面直角坐标系内一点A(2,-5)关于原点对称点的坐标是( )
| A. | (5,-2) | B. | (-2,5) | C. | (-2,-5) | D. | (2,5) |
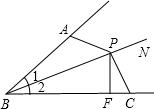 已知:如图,∠1=∠2,P为BN上的一点,PF⊥BC于F,PA=PC,
已知:如图,∠1=∠2,P为BN上的一点,PF⊥BC于F,PA=PC,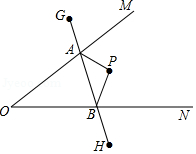 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为14,则△PAB的周长为14.
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为14,则△PAB的周长为14.