题目内容
2.若(x2+y2)2-3x2-3y2-4=0,则x2+y2=4.分析 先设x2+y2=a,代入到原方程中化为关于a的一元二次方程,解这个方程,根据x2+y2>0进行取舍.
解答 解:(x2+y2)2-3x2-3y2-4=0,
(x2+y2)2-3(x2+y2)-4=0,
设x2+y2=a,则原方程可化为:
a2-3a-4=0,
(a-4)(a+1)=0,
a=4或-1,
即x2+y2=4或-1,
∵x2+y2>0,
∴x2+y2=4,
故答案为4.
点评 本题考查了利用换元法解方程,换元的实质是转化,关键是构造元和设元,一般思路为:运用整体换元法,在已知或者未知中,某个代数式几次出现,而用一个字母来代替它,从而简化问题,得出结论.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
10. 小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )
小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )
 小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )
小明在做选择题“如图,四边形ABCD中,∠A=45°,∠B=∠D=90°,AD=2,CD=1,则BC的长为多少”时遇到了困难.小明通过度量发现,试题给出的图形中,AD=3cm,BC=1.05cm,且各角度符合条件,因此小明猜想下列选项中最有可能正确的是( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$+1 |
11.下列性质中,矩形具有但菱形不一定具有的是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | C. | 对角线相等 | D. | 对边平行 |
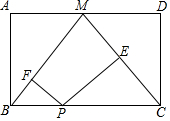 如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MC,PF⊥MB,垂足分别为E,F,当AB,BC满足什么条件时,四边形PEMF为矩形?试加以证明.
如图,M是矩形ABCD的边AD的中点,P为BC上一点,PE⊥MC,PF⊥MB,垂足分别为E,F,当AB,BC满足什么条件时,四边形PEMF为矩形?试加以证明.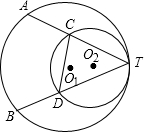 已知:如图,⊙O1与⊙O2内切于点T,⊙O1的弦TA、TB交⊙O2于点C和D,若DC=5,$\frac{TC}{TA}$=$\frac{2}{3}$,求AB的长.
已知:如图,⊙O1与⊙O2内切于点T,⊙O1的弦TA、TB交⊙O2于点C和D,若DC=5,$\frac{TC}{TA}$=$\frac{2}{3}$,求AB的长.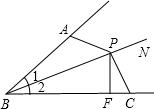 已知:如图,∠1=∠2,P为BN上的一点,PF⊥BC于F,PA=PC,
已知:如图,∠1=∠2,P为BN上的一点,PF⊥BC于F,PA=PC,