题目内容
10.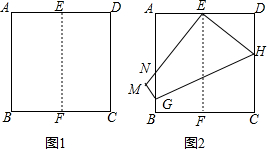 如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N.若AD=2,则MN=$\frac{1}{3}$.
如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N.若AD=2,则MN=$\frac{1}{3}$.
分析 设正方形的边长为2a,DH=x,表示出CH,再根据翻折变换的性质表示出DE、EH,然后利用勾股定理列出方程求出x,再根据相似三角形的判定性质,可得NE的长,根据线段的和差,可得答案.
解答 解:设DH=x,CH=2-x,
由翻折的性质,DE=1,
EH=CH=2-x,
在Rt△DEH中,DE2+DH2=EH2,
即12+x2=(2-x)2,
解得x=$\frac{3}{4}$,EH=2-x=$\frac{5}{4}$.
∵∠MEH=∠C=90°,
∴∠AEN+∠DEH=90°,
∵∠ANE+∠AEN=90°,
∴∠ANE=∠DEH,
又∠A=∠D,
∴△ANE∽△DEH,
$\frac{AE}{DH}$=$\frac{EN}{EH}$,即$\frac{EN}{\frac{5}{4}}$=$\frac{1}{\frac{3}{4}}$,
解得EN=$\frac{5}{3}$,
MN=ME-NE=2-$\frac{5}{3}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题考查了翻折变换的性质,勾股定理的应用,锐角三角函数,设出DH的长,然后利用勾股定理列出方程是解题的关键,也是本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.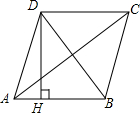 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )| A. | $\frac{24}{5}$ | B. | $\frac{12}{5}$ | C. | 5 | D. | 4 |
15.为了解七年级学生上学期参加社会实践活动的情况,随机抽查A市七年级部分学生参加社会实践活动天数,并根据抽查结果制作了如下不完整的频数分布表和条形统计图.
A市七年级部分学生参加社会实践活动天数的频数分布表
A市七年级部分学生参加社会实践活动天数的条形统计图
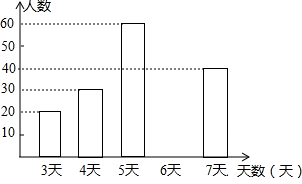
根据以上信息,解答下列问题;
(1)求出频数分布表中a的值,并补全条形统计图.
(2)A市有七年级学生20000人,请你估计该市七年级学生参加社会实践活动不少于5天的人数.
A市七年级部分学生参加社会实践活动天数的频数分布表
| 天数 | 频数 | 频率 |
| 3 | 20 | 0.10 |
| 4 | 30 | 0.15 |
| 5 | 60 | 0.30 |
| 6 | a | 0.25 |
| 7 | 40 | 0.20 |

根据以上信息,解答下列问题;
(1)求出频数分布表中a的值,并补全条形统计图.
(2)A市有七年级学生20000人,请你估计该市七年级学生参加社会实践活动不少于5天的人数.
2.下列图案中,是轴对称图形但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
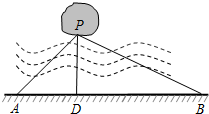 如图,宁波市共湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请帮助小张求出小桥PD的长.($\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)
如图,宁波市共湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请帮助小张求出小桥PD的长.($\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)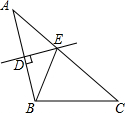 如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为13.
如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为13.