题目内容
18.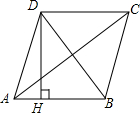 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )| A. | $\frac{24}{5}$ | B. | $\frac{12}{5}$ | C. | 5 | D. | 4 |
分析 根据菱形性质求出AO=4,OB=3,∠AOB=90°,根据勾股定理求出AB,再根据菱形的面积公式求出即可.
解答 解:
∵四边形ABCD是菱形,
∴AO=OC,BO=OD,AC⊥BD,
∵AC=8,DB=6,
∴AO=4,OB=3,∠AOB=90°,
由勾股定理得:AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵S菱形ABCD=$\frac{1}{2}×AC×BD=AB×DH$,
∴$\frac{1}{2}×8×6=5×DH$,
∴DH=$\frac{24}{5}$,
故选A.
点评 本题考查了勾股定理和菱形的性质的应用,能根据菱形的性质得出S菱形ABCD=$\frac{1}{2}×AC×BD=AB×DH$是解此题的关键.

练习册系列答案
相关题目
8.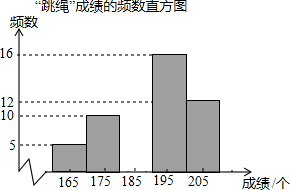 某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:
某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:
“跳绳”成绩的频数表
根据图表解决下列问题:
(1)本次抽样调查的样本容量是50,频数表中,a=0.2,b=7c=0.32;
(2)数据分组的组距是10,本次调查的个体是被抽到的每名九年级学生的跳绳成绩;
(3)补全频数直方图;
(4)“跳绳”数在180以上,则此项成绩可得满分,请估计全校九年级有多少学生在此项成绩中获满分.
 某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:
某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:“跳绳”成绩的频数表
| 组别 | 组中值(个) | 频数 | 频率 |
| A | 165 | 5 | 0.1 |
| B | 175 | 10 | a |
| C | 185 | b | 0.14 |
| D | 195 | 16 | c |
| E | 205 | 12 | 0.24 |
(1)本次抽样调查的样本容量是50,频数表中,a=0.2,b=7c=0.32;
(2)数据分组的组距是10,本次调查的个体是被抽到的每名九年级学生的跳绳成绩;
(3)补全频数直方图;
(4)“跳绳”数在180以上,则此项成绩可得满分,请估计全校九年级有多少学生在此项成绩中获满分.
8.下列运算正确的是( )
| A. | x4+x2=x6 | B. | x2•x3=x6 | C. | (x2)3=x6 | D. | x2-y2=(x-y)2 |
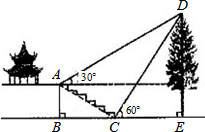 如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
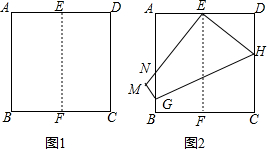 如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N.若AD=2,则MN=$\frac{1}{3}$.
如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N.若AD=2,则MN=$\frac{1}{3}$.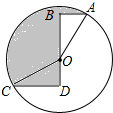 如图,⊙O的半径为2,点A、C在⊙O上,线段BD经过圆心O,∠ABD=∠CDB=90°,AB=1,CD=$\sqrt{3}$,则图中阴影部分的面积为$\frac{5}{3}$π.
如图,⊙O的半径为2,点A、C在⊙O上,线段BD经过圆心O,∠ABD=∠CDB=90°,AB=1,CD=$\sqrt{3}$,则图中阴影部分的面积为$\frac{5}{3}$π.