题目内容
3.已知二次函数y=-x2-x+2.(1)求它的图象的开口方向、对称轴和顶点坐标;
(2)在图示的坐标系中画出函数y=-x2-x+2的图象;
(3)这个函数有最大值还是最小值?最大值或最小值是多少?
(4)当x在什么范围内取值时,y随x的增大而减小?
分析 (1)先把抛物线解析式配成顶点式,然后根据二次函数性质可确定抛物线的开口方向、对称轴和顶点坐标;
(2)利用描点法画出二次函数图象;
(3)、(4)根据二次函数的性质求解.
解答 解:(1)y=-x2-x+2=-(x+$\frac{1}{2}$)2+$\frac{9}{4}$,
所以二次函数的开口向下,对称轴为直线x=-$\frac{1}{2}$,顶点坐标为(-$\frac{1}{2}$,$\frac{9}{4}$);
(2)如图,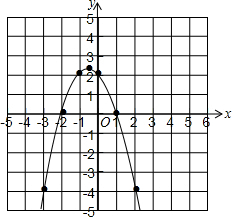
(3)这个函数有最大值,最大值为$\frac{9}{4}$;
(4)当x>-$\frac{1}{2}$时,y随x的增大而减小.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-$\frac{b}{2a}$时,y随x的增大而减小;x>-$\frac{b}{2a}$时,y随x的增大而增大;x=-$\frac{b}{2a}$时,y取得最小值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-$\frac{b}{2a}$时,y随x的增大而增大;x>-b2a时,y随x的增大而减小;x=-$\frac{b}{2a}$时,y取得最大值$\frac{4ac-{b}^{2}}{4a}$,即顶点是抛物线的最高点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.若$\sqrt{2m+n}$与$\root{m-n-1}{m+5}$是同类二次根式,则$\sqrt{m+n}$的值为( )
| A. | 1 | B. | 4 | C. | 5 | D. | $\sqrt{5}$ |
11.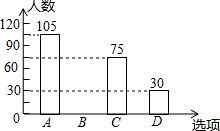 某校决定在6月8日“世界海洋日”开展系列海洋知识的宣传活动,活动有A.唱歌、B.舞蹈、C.绘画、D.演讲四项宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:
某校决定在6月8日“世界海洋日”开展系列海洋知识的宣传活动,活动有A.唱歌、B.舞蹈、C.绘画、D.演讲四项宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:
请结合统计图表,回答下列问题:
(1)本次抽查的学生共300人,a=30%,并将条形统计图补充完整;
(2)如果该校学生有1800人,请你估计该校喜欢“唱歌”这项宣传方式的学生约有多少人?
(3)学校采用抽签方式让每班在A、B、C、D四项宣传方式中随机抽取两项进行展示,请用树状图或列表法求某班所抽到的两项方式恰好是“唱歌”和“舞蹈”的概率.
 某校决定在6月8日“世界海洋日”开展系列海洋知识的宣传活动,活动有A.唱歌、B.舞蹈、C.绘画、D.演讲四项宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:
某校决定在6月8日“世界海洋日”开展系列海洋知识的宣传活动,活动有A.唱歌、B.舞蹈、C.绘画、D.演讲四项宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:| 选项 | 方式 | 百分比 |
| A | 唱歌 | 35% |
| B | 舞蹈 | a |
| C | 绘画 | 25% |
| D | 演讲 | 10% |
(1)本次抽查的学生共300人,a=30%,并将条形统计图补充完整;
(2)如果该校学生有1800人,请你估计该校喜欢“唱歌”这项宣传方式的学生约有多少人?
(3)学校采用抽签方式让每班在A、B、C、D四项宣传方式中随机抽取两项进行展示,请用树状图或列表法求某班所抽到的两项方式恰好是“唱歌”和“舞蹈”的概率.
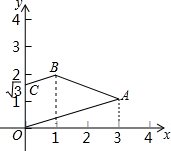 如图,A,B,C三点的坐标分别为(3,1),(1,2),(0,$\sqrt{3}$),试求四边形OABC的面积.
如图,A,B,C三点的坐标分别为(3,1),(1,2),(0,$\sqrt{3}$),试求四边形OABC的面积.