Question

7．如图，直线l₁∥l₂，⊙O与l₁和l₂分别相切于点A和点B．点M和点N分别是l₁和l₂上的动点，MN沿l₁和l₂平移．⊙O的半径为1，∠1=60°．有下列结论：①MN=$\frac{4\sqrt{3}}{3}$；②若MN与⊙O相切，则AM=$\sqrt{3}$；③若∠MON=90°，则MN与⊙O相切；④l₁和l₂的距离为2，其中正确的有（　　）

• A． 4个
• B． 3个
• C． 2个
• D． 1个．

Answer 1

分析 首先过点N作NC⊥AM于点C，直线l₁∥l₂，⊙O与l₁和l₂分别相切于点A和点B，⊙O的半径为1，易求得MN=$\frac{CN}{sin60°}$=$\frac{4\sqrt{3}}{3}$，l₁和l₂的距离为2；若∠MON=90°，连接NO并延长交MA于点C，易证得CO=NO，继而可得即O到MN的距离等于半径，可证得MN与⊙O相切；由题意可求得若MN与⊙O相切，则AM=$\sqrt{3}$或$\frac{\sqrt{3}}{3}$．

解答 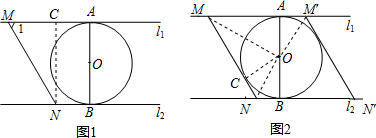解：如图1，过点N作NC⊥AM于点C，
∵直线l₁∥l₂，⊙O与l₁和l₂分别相切于点A和点B，⊙O的半径为1，
∴CN=AB=2，
∵∠1=60°，
∴MN=$\frac{CN}{sin60°}$=$\frac{4\sqrt{3}}{3}$，
故①与④正确；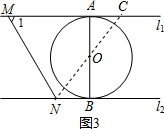
如图3，
若∠MON=90°，连接NO并延长交MA于点C，则△AOC≌△BON，
故CO=NO，△MON≌△MOM′，故MN上的高为1，即O到MN的距离等于半径．
故③正确；
如图2，∵MN是切线，⊙O与l₁和l₂分别相切于点A和点B，
∴∠AMO=$\frac{1}{2}$∠1=30°，
∴AM=$\sqrt{3}$；
∵∠AM′O=60°，
∴AM′=$\frac{\sqrt{3}}{3}$，
∴若MN与⊙O相切，则AM=$\sqrt{3}$或$\frac{\sqrt{3}}{3}$；
故②错误．
故选B．

点评 此题考查了切线的判定与性质、全等三角形的判定与性质以及三角函数等知识．此题难度较大，注意掌握数形结合思想与分类讨论思想的应用．