题目内容
12.(1)82m×4n÷2m-n(2)6m•362m÷63m-2
(3)(a4•a3÷a2)3
(4)(-10)2+(-10)0+10-2×(-102)
(5)($\frac{3}{4}$x6y5+$\frac{6}{5}$x5y4-$\frac{9}{10}$x4y3)÷$\frac{3}{5}$x3y3
(6)$\frac{1}{2}$x-(2x-$\frac{1}{3}$y2)+($\frac{1}{2}$x-$\frac{1}{3}$y2)
(7)2-[x-$\frac{1}{2}$(x-1)]-$\frac{2}{3}$(x-1)
(8)5xy2-{2x2y-[3xy2-(xy2-2x2y)]÷(-$\frac{1}{2}$xy)}.
分析 (1)根据同底数幂的乘除法进行计算即可;
(2)根据同底数幂的乘除法进行计算即可;
(3)根据同底数幂的乘除法进行计算即可;
(4)根据同底数幂的乘除法、合并同类项进行计算即可;
(5)根据多项式除以单项式进行计算即可;
(6)根据合并同类项得法则进行计算即可;
(7)先去括号,再根据合并同类项得法则进行计算即可;
(8)根据运算顺序,先算乘除,再算加减,有括号的先算括号里面的.
解答 解:(1)原式=26m×22n÷2m-n
=26m+2n-m+n
=25m+3n;
(2)原式=6m•64m÷63m-2
=6m+4m-3m+2
=62m+2;
(3)原式=(a4+3-2)3
=a15;
(4)原式=100+1-1
=100;
(5)原式$\frac{3}{4}$x6y5÷$\frac{3}{5}$x3y3+$\frac{6}{5}$x5y4÷$\frac{3}{5}$x3y3-$\frac{9}{10}$x4y3÷$\frac{3}{5}$x3y3
=$\frac{5}{4}$x3y2+2x2y-$\frac{3}{2}$x;
(6)原式=$\frac{1}{2}$x-2x+$\frac{1}{3}$y2+$\frac{1}{2}$x-$\frac{1}{3}$y2
=-x;
(7)原式=2-x+$\frac{1}{2}$x-$\frac{1}{2}$-$\frac{2}{3}$x+$\frac{2}{3}$
=-$\frac{7}{6}$x+$\frac{13}{6}$;
5xy2-{2x2y-[3xy2-(xy2-2x2y)]÷(-$\frac{1}{2}$xy)}.(8)原式=5xy2-(2x2y-3xy2+xy2-2x2y)÷(-$\frac{1}{2}$xy)
=5xy2-4y.
点评 本题考查了整式的混合运算,涉及的知识点:同底数幂的乘法、除法、合并同类项、多项式除以单项式,是中考题的常见题型,要熟练掌握.

| A. | 121(1+x)=100 | B. | 121(1-x)=100 | C. | 121(1-x)2=100 | D. | 100(1+x)2=121 |
| A. | $\frac{1}{7}$ | B. | -$\frac{1}{7}$ | C. | 7 | D. | -7 |
 如图,已知△OAB的顶点A(-6,0),B(0,2),O是坐标原点,将△OAB绕点O按顺时针旋转90°,得到△ODC.抛物线y=ax2+bx+c经过A,D,C三点.
如图,已知△OAB的顶点A(-6,0),B(0,2),O是坐标原点,将△OAB绕点O按顺时针旋转90°,得到△ODC.抛物线y=ax2+bx+c经过A,D,C三点.  如图,在△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD与CE相交于点F,FG⊥AB,FH⊥BC,垂足分别为G,H,求证:FE=FD.
如图,在△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD与CE相交于点F,FG⊥AB,FH⊥BC,垂足分别为G,H,求证:FE=FD. 如图,P是正三角形ABC内的一点,若将△PAC绕点A逆时针旋转后,得到△P′AB,
如图,P是正三角形ABC内的一点,若将△PAC绕点A逆时针旋转后,得到△P′AB,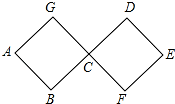 如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.
如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.