题目内容
18.阅读材料:材料1:x1,x2是一元二次方程ax2+bx+c=0的两根,则x1,x2与系数a,b,c有如下关系:
$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=-\frac{b}{a}}\\{{x}_{1}•{x}_{2}=\frac{c}{a}}\end{array}\right.$,我们称之为韦达定理.
材料2:设a2+1=3a,b2+1=3b.且a≠b,则代数式$\frac{1}{a}$+$\frac{1}{b}$的值为3
解:对于a2+1=3a,b2+1=3b两个方程.我们可以把a,b看作是一元二次方程x2-3x+1=0两个根,由韦达定理可得:a+b=3,ab=1
所以:$\frac{1}{a}$+$\frac{1}{b}$=$\frac{b+a}{ab}$=$\frac{3}{1}$=3
回答下列问题:
(1)设a2-2a-1=0,b2-2b-1=0,且a≠b,则a+b=2
(2)设m2-2m+a=0,n4-2n2+a=0,且$\frac{1}{{n}^{2}}$+$\frac{1}{m}$=-2.则a=-1
(3)已知a,b是正整数,且ab+a+b=9,a2b+ab2=20,求a2+b2的值.
分析 (1)直接利用韦达定理,把a,b看作是一元二次方程x2-2x-1=0两个根求出答案;
(2)接利用韦达定理,把m,n2看作是一元二次方程x2-2x+a=0两个根求出答案;
(3)利用已知得出ab,a+b,看作是一元二次方程x2-9x+20=0两个根,进而得出答案.
解答 解:(1)对于a2-2a-1=0,b2-2b-1=0两个方程.
我们可以把a,b看作是一元二次方程x2-2x-1=0两个根,
由韦达定理可得:a+b=2;
故答案为:2;
(2)对于m2-2m+a=0,n4-2n2+a=0,两个方程.
我们可以把m,n2看作是一元二次方程x2-2x+a=0两个根,
由韦达定理可得:$\frac{1}{{n}^{2}}$+$\frac{1}{m}$=$\frac{{n}^{2}+m}{{n}^{2}m}$=$\frac{2}{a}$=-2,
解得:a=-1;
故答案为:-1;
(3)∵ab+a+b=9,a2b+ab2=ab(a+b)=20,
∴设ab,a+b,看作是一元二次方程x2-9x+20=0两个根,由a,b是正整数,
解得:a+b=5,ab=4,
∴a2+b2=(a+b)2-2ab=25-8=17.
点评 此题主要考查了根与系数的关系,正确应用韦达定理是解题关键.

练习册系列答案
相关题目
13.函数y=2x-1中,自变量x的取值范围是x>-1,则函数y的取值范围为( )
| A. | y<-3 | B. | y>-3 | C. | y>-1 | D. | y<-1 |
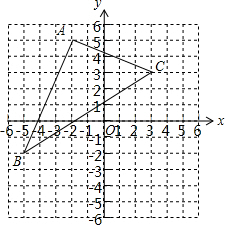 如图,已知△ABC各顶点的坐标分别为A(-2,5)B(-5,-2),C(3,3).将△ABC先向右平移4个单位长度,再向下平移3个单位长度,得到△A′B′C′.
如图,已知△ABC各顶点的坐标分别为A(-2,5)B(-5,-2),C(3,3).将△ABC先向右平移4个单位长度,再向下平移3个单位长度,得到△A′B′C′.