题目内容
9.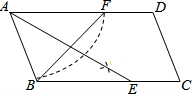 如图,平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为8.
如图,平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为8.
分析 由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=$\frac{1}{2}$BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.
解答 解:连结EF,AE与BF交于点O,如图,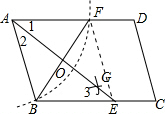
∵AB=AF,AO平分∠BAD,
∴AO⊥BF,BO=FO=$\frac{1}{2}$BF=3,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
而BO⊥AE,
∴AO=OE,
在Rt△AOB中,AO=$\sqrt{A{B}^{2}-O{B}^{2}}$=4,
∴AE=2AO=8.
故答案为:8.
点评 本题考查了平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.也考查了等腰三角形的判定与性质和基本作图.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
14.6的负倒数是( )
| A. | -6 | B. | 6 | C. | $\frac{1}{6}$ | D. | $-\frac{1}{6}$ |
1.若关于x的不等式(3-m)x<3-m的解集为x>1,则m的取值范围是( )
| A. | m<0 | B. | m>0 | C. | m>3 | D. | m<3 |
10.已知a为任意实数,且M=2a-2,N=a2-1,则M,N的大小关系为( )
| A. | M≤N | B. | M≥N | C. | M=N | D. | 不能确定 |
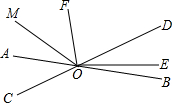 如图,直线AB,CD相交于点O,∠DOE:∠BOE=3:1,OF平分∠AOD,
如图,直线AB,CD相交于点O,∠DOE:∠BOE=3:1,OF平分∠AOD,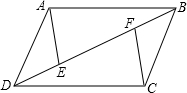 如图,已知四边形ABCD为平行四边形,E、F为对角线BD上的两点,且DF=BE,连接AE,CF.
如图,已知四边形ABCD为平行四边形,E、F为对角线BD上的两点,且DF=BE,连接AE,CF.
 在四边形ABCD中,AB=AD,请利用尺规在CD边上求作一点P,使得S△PAB=S△PAD,(保留作图痕迹,不写作法).
在四边形ABCD中,AB=AD,请利用尺规在CD边上求作一点P,使得S△PAB=S△PAD,(保留作图痕迹,不写作法).