题目内容
3.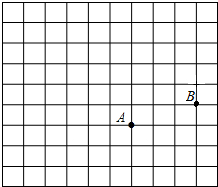 如图,在正方形网格中,每个小正方形的边长都为1,点A点B在网格中的位置如图所示.
如图,在正方形网格中,每个小正方形的边长都为1,点A点B在网格中的位置如图所示.(1)建立适当的平面直角坐标系,使点A点B的坐标分别为(1,2)(4,3);
(2)点C的坐标为(3,6),在平面直角坐标系中找到点C的位置,连接AB、BC、CA,则∠ACB=45°;
(3)将点A、B、C的横坐标都乘以-1,纵坐标不变,分别得到点A1、B1、C1,在图中找到点A1、B1、C1并顺次连接点A1、B1、C1,得到△A1B1C1,则这两个三角形关于y轴对称.
分析 (1)根据A、B两点的坐标分别为(1,2)(4,3)建立平面直角坐标系即可;
(2)在坐标系内找出C点,连接AB、BC、CA,根据求出各边的长,判断出△ABC的形状,进而可得出结论;
(3)在图中找到点A1、B1、C1并顺次连接点A1、B1、C1即可得出结论.
解答 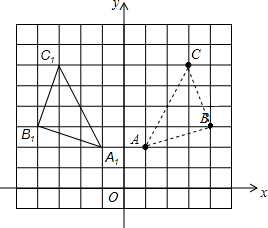 解:(1)如图所示;
解:(1)如图所示;
(2)如图所示,
∵AC2=42+22=20,BC2=12+32=10,AB2=12+32=10,
∴△ABC是等腰直角三角形,
∴∠ACB=45°.
故答案为:45;
(3)如图所示,由图可知△ABC与△A1B1C1关于y轴对称.
故答案为:y轴.
点评 本题考查的是作图-轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
8. 如图所示,已知AB=DB,∠ABD=∠CBE,添加下列哪一个条件后,仍不能证明△ABC≌△DBE的是( )
如图所示,已知AB=DB,∠ABD=∠CBE,添加下列哪一个条件后,仍不能证明△ABC≌△DBE的是( )
 如图所示,已知AB=DB,∠ABD=∠CBE,添加下列哪一个条件后,仍不能证明△ABC≌△DBE的是( )
如图所示,已知AB=DB,∠ABD=∠CBE,添加下列哪一个条件后,仍不能证明△ABC≌△DBE的是( )| A. | DE=AC | B. | ∠BDE=∠BAC | C. | ∠DEB=∠ACB | D. | BE=BC |
15. 如图,圆O中,圆弧AB=圆弧AC,∠C=80°,则∠A=( )
如图,圆O中,圆弧AB=圆弧AC,∠C=80°,则∠A=( )
 如图,圆O中,圆弧AB=圆弧AC,∠C=80°,则∠A=( )
如图,圆O中,圆弧AB=圆弧AC,∠C=80°,则∠A=( )| A. | 40° | B. | 30° | C. | 20° | D. | 50° |
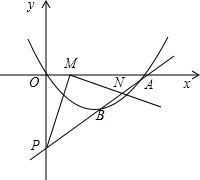 如图,抛物线y=ax2+bx+c过原点,且与直线y=mx+n交于A(8,0)、B(4,-3)两点,直线AB与y轴相交于点P,点M为线段OA上一动点,∠PMN为直角,边MN与AP相交于点N,设OM=t.
如图,抛物线y=ax2+bx+c过原点,且与直线y=mx+n交于A(8,0)、B(4,-3)两点,直线AB与y轴相交于点P,点M为线段OA上一动点,∠PMN为直角,边MN与AP相交于点N,设OM=t.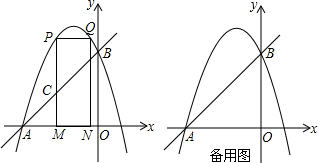
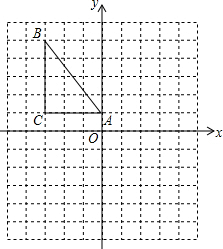 如图,已知Rt△ABC中,∠C=90°,AC=3,BC=4,在如图的坐标系中,点A的坐标为(0,1),点B的坐标为(-3,5),AC与x轴平行.
如图,已知Rt△ABC中,∠C=90°,AC=3,BC=4,在如图的坐标系中,点A的坐标为(0,1),点B的坐标为(-3,5),AC与x轴平行.