题目内容
13.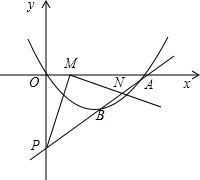 如图,抛物线y=ax2+bx+c过原点,且与直线y=mx+n交于A(8,0)、B(4,-3)两点,直线AB与y轴相交于点P,点M为线段OA上一动点,∠PMN为直角,边MN与AP相交于点N,设OM=t.
如图,抛物线y=ax2+bx+c过原点,且与直线y=mx+n交于A(8,0)、B(4,-3)两点,直线AB与y轴相交于点P,点M为线段OA上一动点,∠PMN为直角,边MN与AP相交于点N,设OM=t.(1)求抛物线和直线的解析式;
(2)当t为何值时,△MAN为等腰三角形;
(3)当t为何值时,以线段PN为直径的圆与x轴相切?并求此时圆的直径PN的长.
分析 (1)直接根据待定系数法求出二次函数与一次函数的解析式;
(2)若△MAN为等腰三角形,则只能是∠NMA=∠NAM,证明三角形△OPM∽△OAP,进而求出OM的长,即t的值;
(3)存在以线段PN为直径的圆与x轴相切,设以PN为直径作圆Q,若圆Q与x轴相切,则切点为M,连接MQ,根据△AMQ∽△AOP求出QM的长,再结合勾股定理求出AM的长,进而求出OM的值,即t的值.
解答 解:(1)∵抛物线y=ax2+bx+c过原点且经过A(8,0)、B(4,3),
∴$\left\{\begin{array}{l}{64a+8b+c=0}\\{16a+4b+c=-3}\\{c=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=\frac{3}{16}}\\{b=-\frac{3}{2}}\\{c=0}\end{array}\right.$,
∴抛物线解析式为y=$\frac{3}{16}$x2-$\frac{3}{2}$x,
∵直线y=mx+n交于A(8,0)、B(4,-3)两点,
∴$\left\{\begin{array}{l}{8m+n=0}\\{4m+n=-3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=\frac{3}{4}}\\{n=-6}\end{array}\right.$,
∴直线AB解析式为y=$\frac{3}{4}$x-6;
(2)若△MAN为等腰三角形,则只能是∠NMA=∠NAM,
∵∠PMN=90°,
∴∠AMN+∠PMO=90°,
∵∠OPM+∠OMP=90°,
∴∠OPM=∠AMN,
∵∠NMA=∠NAM,
∴∠OPM=∠MAN,
∴△OPM∽△OAP,
∴$\frac{OP}{OA}=\frac{OM}{OP}$,
∴OM=$\frac{36}{8}$=$\frac{9}{2}$,
即t=$\frac{9}{2}$时,△MAN为等腰三角形;
(3)存在以线段PN为直径的圆与x轴相切,
设以PN为直径作圆Q,
若圆Q与x轴相切,则切点为M,连接MQ,
∵△AMQ∽△AOP,
∴$\frac{QM}{PO}$=$\frac{AQ}{AP}$,
∴$\frac{QM}{PO}$=$\frac{AP-QM}{AP}$,
∴$\frac{QM}{6}$=$\frac{10-QM}{10}$,
∴QM=$\frac{15}{4}$,
∴AQ=10-$\frac{15}{4}$=$\frac{25}{4}$,
AM=$\sqrt{(\frac{25}{4})^{2}-(\frac{15}{4})^{2}}$=5,
∴OM=3,
即t=3时,线段PN为直径的圆与x轴相切
此时圆的直径PN=2QM=$\frac{15}{2}$.
点评 本题主要考查了二次函数的综合题,涉及到待定系数法求函数解析式、相似三角形的判定与性质以及圆的相关知识,解答本题的关键是多次利用相似三角形的性质求线段的长,此题有一定的难度.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 以上都不对 |
 如图,在正方形ABCD中,AB=4,将△ADC绕点A顺时针旋转α(0<α<45°),记旋转后的三角形为△AD′C′,过点B作BE⊥AC′于点E,延长BE交射线AD′于点F,连接DF,取AB中点H,连接HE,在旋转过程中,当HE⊥BD时,(BE+DF)2的值为8+4$\sqrt{2}$.
如图,在正方形ABCD中,AB=4,将△ADC绕点A顺时针旋转α(0<α<45°),记旋转后的三角形为△AD′C′,过点B作BE⊥AC′于点E,延长BE交射线AD′于点F,连接DF,取AB中点H,连接HE,在旋转过程中,当HE⊥BD时,(BE+DF)2的值为8+4$\sqrt{2}$.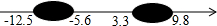 如图,一滴墨水洒在一个数轴上,根据图中标出的数据,被墨水盖住的整数共有个13个.
如图,一滴墨水洒在一个数轴上,根据图中标出的数据,被墨水盖住的整数共有个13个.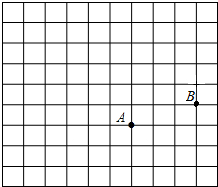 如图,在正方形网格中,每个小正方形的边长都为1,点A点B在网格中的位置如图所示.
如图,在正方形网格中,每个小正方形的边长都为1,点A点B在网格中的位置如图所示.