题目内容
8. 如图所示,已知AB=DB,∠ABD=∠CBE,添加下列哪一个条件后,仍不能证明△ABC≌△DBE的是( )
如图所示,已知AB=DB,∠ABD=∠CBE,添加下列哪一个条件后,仍不能证明△ABC≌△DBE的是( )| A. | DE=AC | B. | ∠BDE=∠BAC | C. | ∠DEB=∠ACB | D. | BE=BC |
分析 利用∠ABD=∠CBE,加上∠ABC=∠DBE,则利用全等三角形的判定方法对各选项进行判断.
解答 解:∵∠ABD=∠CBE,
∴∠ABC=∠DBE,
∵AB=DB,
∴BC=BE时,可利用“SAS”判定△ABC≌△DBE;
当∠BDE=∠BAC时,可利用“ASA”判定△ABC≌△DBE;
当∠DEB=∠ACB时,可利用“AAS”判定△ABC≌△DBE.
故选A.
点评 本题考查了三角形全等的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
17.三元一次方程组$\left\{\begin{array}{l}{3x-2y=5}\\{x+y+z=2}\\{z=2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=1}\\{z=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\\{z=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-1}\\{y=1}\\{z=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\\{z=2}\end{array}\right.$ |
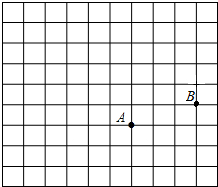 如图,在正方形网格中,每个小正方形的边长都为1,点A点B在网格中的位置如图所示.
如图,在正方形网格中,每个小正方形的边长都为1,点A点B在网格中的位置如图所示.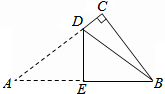 如图,已知Rt△ABC中,∠C=90°,AB=10cm,BC=6cm.现将△ABC沿折痕DE进行折叠,使顶点A,B重合,则△DCB的周长等于14cm.
如图,已知Rt△ABC中,∠C=90°,AB=10cm,BC=6cm.现将△ABC沿折痕DE进行折叠,使顶点A,B重合,则△DCB的周长等于14cm. 如图,△ABC三定点在圆O上,AC是圆O的直径,∠C=52°,∠ABC平分线BD交圆O于点D,求∠BAD的度数.
如图,△ABC三定点在圆O上,AC是圆O的直径,∠C=52°,∠ABC平分线BD交圆O于点D,求∠BAD的度数.