题目内容
11.从2开始,连续的偶数相加,它们和的情况如下表:加数的个数nS
1 2=1×2
2 2+4=6=2×3
3 2+4+6=12=3×4
4 2+4+6+8=20=4×5
5 2+4+6+8+10=30=5×6
(1)若n=8时,则 S的值为72.
(2)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=n(n+1).
(3)根据上题的规律计算2+4+6+8+10+…+98+100 的值.
分析 (1)根据所给的式子可得S与n之间的关系为S=n(n+1),再把n=8代入计算即可;
(2)根据(1)得出的规律可直接得出答案;
(3)根据(2)得出的规律,代值计算即可.
解答 解:(1)∵1个最小的连续偶数相加时,S=1×(1+1),
2个最小的连续偶数相加时,S=2×(2+1),
3个最小的连续偶数相加时,S=3×(3+1),
∴n个最小的连续偶数相加时,S=n(n+1);
∴n=8时,则 S的值为S=8×(8+1)=72;
故答案为:72;
(2)①根据(1)得:
S=2+4+6+8+…+2n=n(n+1);
故答案为:n(n+1);
(3)根据(2)可得:
2+4+6+8+10+…+98+100=50×51=2550.
点评 此题考查了数字的变化类,是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.

练习册系列答案
相关题目
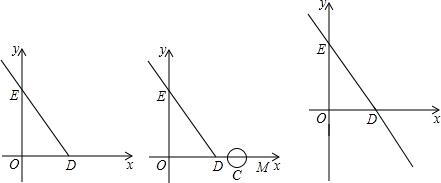
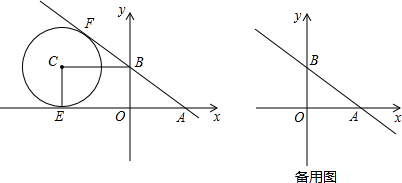
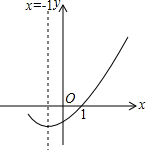 如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0,其中正确的命题是( )
如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0,其中正确的命题是( )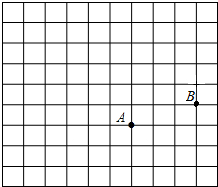 如图,在正方形网格中,每个小正方形的边长都为1,点A点B在网格中的位置如图所示.
如图,在正方形网格中,每个小正方形的边长都为1,点A点B在网格中的位置如图所示. 如图,△ABC三定点在圆O上,AC是圆O的直径,∠C=52°,∠ABC平分线BD交圆O于点D,求∠BAD的度数.
如图,△ABC三定点在圆O上,AC是圆O的直径,∠C=52°,∠ABC平分线BD交圆O于点D,求∠BAD的度数.