题目内容
10. 如图,△ABC与△BDE都是等边三角形,且点A、B、D在同一条直线上.请判断AE与CD的大小关系,并证明.
如图,△ABC与△BDE都是等边三角形,且点A、B、D在同一条直线上.请判断AE与CD的大小关系,并证明.
分析 AE=CD,根据等边三角形的性质求出△ABE≌△CBD,再根据全等三角形的性质解答即可.
解答 解:AE=CD,理由如下:
∵△ABC和△BDE分别是等边三角形,
∴AB=CB,BE=BD,
∴∠ABC=∠DBE=60°,
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD,
在△ABE和△CBD中,
$\left\{\begin{array}{l}{AB=CB}\\{∠ABE=∠CBD}\\{BE=BD}\end{array}\right.$,
∴△ABE≌△CBD(SAS),
∴AE=CD.
点评 本题考查了全等三角形的判定与性质,等边三角形的性质,当出现两个等边三角形时,一般要利用等边三角形的边和角从中找到一对全等三角形.

练习册系列答案
相关题目
15.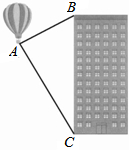 如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为60m,这栋高楼BC的高度为( )
如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为60m,这栋高楼BC的高度为( )
 如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为60m,这栋高楼BC的高度为( )
如图,热气球的探测器显示,从热气球A看一栋楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为60m,这栋高楼BC的高度为( )| A. | 80$\sqrt{3}$m | B. | 60$\sqrt{3}$m | C. | 40$\sqrt{3}$m | D. | 30$\sqrt{3}$m |
18.已知$\sqrt{12a}$是整数,则正整数a的最小值是( )
| A. | 2 | B. | 3 | C. | 6 | D. | 12 |
5. 如图,已知直线a与b相交,若∠1=75°,则∠2的度数为( )
如图,已知直线a与b相交,若∠1=75°,则∠2的度数为( )
 如图,已知直线a与b相交,若∠1=75°,则∠2的度数为( )
如图,已知直线a与b相交,若∠1=75°,则∠2的度数为( )| A. | 75° | B. | 105° | C. | 115° | D. | 无法确定 |
19.下列式子中,不属于二次根式的是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{{a}^{2}}$ | C. | $\sqrt{-7}$ | D. | $\sqrt{\frac{1}{2}}$ |
20.下列命题中,真命题是( )
| A. | 圆周角等于圆心角的一半 | B. | 等弧所对的圆周角相等 | ||
| C. | 平分弦的直径垂直于弦 | D. | 过弦的中点的直线必经过圆心 |