题目内容
4.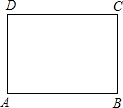 如图,在一张长为9cm,宽为8cm的矩形纸片上,现要剪下一个腰长为5cm的钝角等腰三角形,则剪下的钝角等腰三角形腰上的高为3或4cm,(要求:钝角等腰三角形的一个顶点与矩形的一个顶点重合,其余两个顶点在矩形的边上)
如图,在一张长为9cm,宽为8cm的矩形纸片上,现要剪下一个腰长为5cm的钝角等腰三角形,则剪下的钝角等腰三角形腰上的高为3或4cm,(要求:钝角等腰三角形的一个顶点与矩形的一个顶点重合,其余两个顶点在矩形的边上)
分析 分类讨论:腰在宽BC上时,腰在宽AB上时,根据勾股定理可得答案.
解答 解:腰在宽BC上时,如图: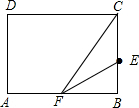
CE=EF=5,
BE=BC-CE=8-5=3.
由勾股定理,得
FB=$\sqrt{E{F}^{2}-B{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4cm,
当腰在宽AB上时,如图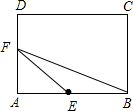 ,
,
BE=EF=5,AE=AB-BE=9-5=4,
由勾股定理,得
AF=$\sqrt{E{F}^{2}-A{E}^{2}}$=$\sqrt{{5}^{2}-{4}^{3}}$=3cm,
故答案为:3或4.
点评 本题考查了等腰三角形的判定,利用了等腰三角形的定义,勾股定理,分类讨论是解题关键,以防遗漏.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
19.在一次学生田径运动会上,参加跳高的15名运动员的成绩如下表所示:
那么这些运动员跳高成绩的众数是( )
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 1 | 3 | 5 | 3 | 2 |
| A. | 3 | B. | 5 | C. | 1.65 | D. | 1.70 |
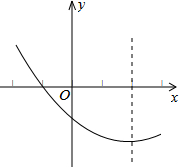 如图抛物线y=ax2+bx+c(a≠0),过点(-1,0),对称轴为直线x=2,则下列结论:
如图抛物线y=ax2+bx+c(a≠0),过点(-1,0),对称轴为直线x=2,则下列结论: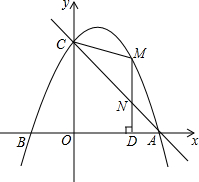 如图,二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过点A,B(-2,0),C(0,4),作直线AC,点M是二次函数图象上的一动点,过点作MD⊥x轴,垂足为点D,交直线AC于点N,连结CM.
如图,二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过点A,B(-2,0),C(0,4),作直线AC,点M是二次函数图象上的一动点,过点作MD⊥x轴,垂足为点D,交直线AC于点N,连结CM.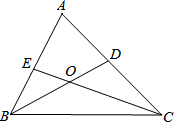 如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的平分线,BD、CE交于点O.
如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的平分线,BD、CE交于点O.