题目内容
17.从背面相同的同一副扑克牌中取出红桃9张,黑桃10张,方块11张,现将这些牌洗匀背面朝上放桌面上.(1)求从中抽出一张是红桃的概率;
(2)现从桌面上先抽掉若干张黑桃,再放入与抽掉的黑桃张数相同的红桃,并洗匀且背面都朝上排开后,随机抽一张是红桃的概率不小于$\frac{2}{5}$,问至少抽掉了多少张黑桃?
(3)若先从桌面上抽掉9张红桃和m(m>6)张黑桃后,再在桌面上抽出一张牌,当m为何值时,事件“再抽出的这张牌是方块”为必然事件?当m为何值时,事件“再抽出的这张牌是方块”为随机事件?并求出这个事件的概率的最小值.
分析 (1)根据题意列式计算即可;
(2)设至少抽掉了x张黑桃,放入x张的红桃,根据题意列不等式即可得到结论;
(3)根据题意即可得到结论.
解答 解:(1)抽出一张是红桃的概率是$\frac{9}{9+10+11}$=$\frac{3}{10}$;
(2)设至少抽掉了x张黑桃,放入x张的红桃,
根据题意得,$\frac{9+x}{9+10+11}$≥$\frac{2}{5}$,
解得:x≥3,
答:至少抽掉了3张黑桃;
(3)当m为10时,事件“再抽出的这张牌是方块”为必然事件,
当m为9,8,7时,事件“再抽出的这张牌是方块”为随机事件事件,
P(最小)=$\frac{11}{(10-7)+11}$=$\frac{11}{14}$.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.同时考查了必然事件、不可能事件与随机事件的定义.

练习册系列答案
相关题目
7.已知m为实数,且sinα、cosα是关于x的方程3x2-mx+1=0的两根,则sin4α+cos4α的值为( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{7}{9}$ | D. | 1 |
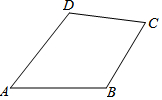 如图,在四边形ABCD中,AB=AD,CB=CD.请你添加一条线把它分成两个全等三角形,并给出证明.
如图,在四边形ABCD中,AB=AD,CB=CD.请你添加一条线把它分成两个全等三角形,并给出证明.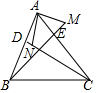 如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是90°.
如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是90°.