题目内容
5. 如图,正方形ABCD边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
如图,正方形ABCD边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.(1)求证:∠HEA=∠CGF;
(2)当AH=DG=2时,求证:菱形EFGH为正方形;
(3)设AH=2,DG=x,△FCG的面积为y,求y与x之间的函数解析式,并直接写出x的取值范围;
(4)求y的最小值.
分析 (1)连接GE,根据正方形的性质和平行线的性质得到∠AEG=∠CGE,根据菱形的性质和平行线的性质得到∠HEG=∠FGE,解答即可;
(2)证明Rt△HAE≌Rt△GDH,得到∠AHE=∠DGH,证明∠GHE=90°,根据正方形的判定定理证明;
(3)作FM⊥DC,证明Rt△AHE≌Rt△GFM,得到MF=AH=2,根据三角形的面积公式得到解析式;
(4)根据一次函数的性质:当k<0时,y随x的增大而减小解答即可.
解答  (1)证明:如图1,连接GE,
(1)证明:如图1,连接GE,
∵AB∥CD,
∴∠AEG=∠CGE,
∵GF∥HE,
∴∠HEG=∠FGE,
∴∠HEA=∠CGF;
(2)证明:∵四边形ABCD是正方形,
∴∠D=∠A=90°,
∵四边形EFGH是菱形,
∴HG=HE,
在Rt△HAE和Rt△GDH中,
$\left\{\begin{array}{l}{AH=DG}\\{HE=HG}\end{array}\right.$,
∴Rt△HAE≌Rt△GDH,
∴∠AHE=∠DGH,又∠DHG+∠DGH=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∴菱形EFGH为正方形;
(3)解:作FM⊥DC,交DC的延长线于M,
在Rt△AHE和Rt△GFM中,
$\left\{\begin{array}{l}{∠A=∠M}\\{∠AEH=∠FGM}\\{HE=FG}\end{array}\right.$,
∴Rt△AHE≌Rt△GFM,
∴MF=AH=2,
∵DG=x,
∴CG=6-x,
∴y=$\frac{1}{2}$×CG×FM=$\frac{1}{2}$×2×(6-x)=6-x(0≤x≤2$\sqrt{6}$);
(4)∵k=-1<0,
∴y随x的增大而减小,
∴x=2$\sqrt{6}$时,y的最小值是6-2$\sqrt{6}$.
点评 本题考查的是正方形的性质、菱形的性质、全等三角形的判定和性质、一次函数解析式的求法和一次函数的性质,正确作出辅助线、灵活运用相关的性质定理和判定定理是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | a2+a2=a4 | B. | a3•a2=a6 | C. | a6÷a2=a4 | D. | (a3)2=a5 |
| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
| A. | x<1 | B. | x>1 | C. | x≠1 | D. | 全体实数 |
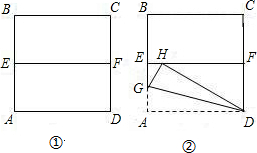 将一张边长为2的正方形纸片ABCD对折,设折痕为EF(如图①);再沿过点D的折痕将角A反折,使得点A落在EF上的点H处(如图②),折痕交AE于点G,则EG的长度是( )
将一张边长为2的正方形纸片ABCD对折,设折痕为EF(如图①);再沿过点D的折痕将角A反折,使得点A落在EF上的点H处(如图②),折痕交AE于点G,则EG的长度是( )| A. | 8-4$\sqrt{3}$ | B. | 4$\sqrt{3}$-6 | C. | 2$\sqrt{3}$-3 | D. | 4-2$\sqrt{3}$ |
| A. | a+2a=3a2 | B. | (a+b)2=a2+b2 | C. | (a2)3=a5 | D. | x7÷x5=x2 |



