题目内容
在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小、质地完全相同,小李从布袋里随机取出一个小球,记下数字为x,小张在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=-x+5图象上的概率.
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=-x+5图象上的概率.
考点:列表法与树状图法,一次函数图象上点的坐标特征
专题:
分析:(1)首先根据题意画出表格,即可得到Q的所以坐标;
(2)然后由表格求得所有等可能的结果与数字x、y满足y=-x+5的情况,再利用概率公式求解即可求得答案
(2)然后由表格求得所有等可能的结果与数字x、y满足y=-x+5的情况,再利用概率公式求解即可求得答案
解答:解:列表得:
(1)点Q所有可能的坐标有:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12种;
(2)∵共有12种等可能的结果,其中在函数y=-x+5图象上的有4种,
即:(1,4),(2,3),(3,2),(4,1)
∴点P(x,y)在函数y=-x+5图象上的概率为:P=
=
.
| (x,y) | 1 | 2 | 3 | 4 |
| 1 | (1,2) | (1,3) | (1,4) | |
| 2 | (2,1) | (2,3) | (2,4) | |
| 3 | (3,1) | (3,2) | (3,4) | |
| 4 | (4,1) | (4,2) | (4,3) |
(2)∵共有12种等可能的结果,其中在函数y=-x+5图象上的有4种,
即:(1,4),(2,3),(3,2),(4,1)
∴点P(x,y)在函数y=-x+5图象上的概率为:P=
| 4 |
| 12 |
| 1 |
| 3 |
点评:此题考查的是用列表法或树状图法求概率与不等式的性质.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
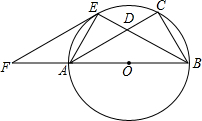 如图,已知以Rt△ABC的边AB为直径作△ABc的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
如图,已知以Rt△ABC的边AB为直径作△ABc的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.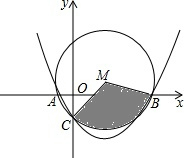 已知抛物线y=ax2+bx-1,经过点A(-1,0),B(m,0)(m>0),且与y轴交于点C.
已知抛物线y=ax2+bx-1,经过点A(-1,0),B(m,0)(m>0),且与y轴交于点C. 如图,在Rt△ABC中,∠ABC=90°,BC=6,AB=8,分别以△ABC两锐角顶点A、C为圆心作等圆,⊙A与⊙C恰好外切,那么图中阴影部分的面积是
如图,在Rt△ABC中,∠ABC=90°,BC=6,AB=8,分别以△ABC两锐角顶点A、C为圆心作等圆,⊙A与⊙C恰好外切,那么图中阴影部分的面积是