题目内容
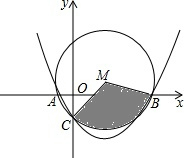 已知抛物线y=ax2+bx-1,经过点A(-1,0),B(m,0)(m>0),且与y轴交于点C.
已知抛物线y=ax2+bx-1,经过点A(-1,0),B(m,0)(m>0),且与y轴交于点C.(1)求抛物线的解析式(用含m的式子表示)
(2)如图所示,⊙M过A、B、C三点,求阴影部分扇形的面积S(用含m的式子表示)
考点:二次函数综合题
专题:
分析:(1)根据所给的A、B的值,代入二次函数,可求出a、b的值,得到二次函数的表达式;
(2)由点的坐标可得到△AOC是等腰直角三角形,从而得到∠CMB=90°,再利用扇形面积公式可计算出面积.
(2)由点的坐标可得到△AOC是等腰直角三角形,从而得到∠CMB=90°,再利用扇形面积公式可计算出面积.
解答:解:(1)依题意得:
,
解得:
,
故抛物线的解析式为:y=
x2+
x-1;
(2)∵x=0时,y=-1,
∴C(0,-1),
∵OA=OC,
∴∠OAC=45°,即∠BAC=45°,
∴∠BMC=2∠OAC=90°.
又∵BC=
,
∴S=
π•MC2=
π×
=
.
|
解得:
|
故抛物线的解析式为:y=
| 1 |
| m |
| 1-m |
| m |

(2)∵x=0时,y=-1,
∴C(0,-1),
∵OA=OC,
∴∠OAC=45°,即∠BAC=45°,
∴∠BMC=2∠OAC=90°.
又∵BC=
| m2+1 |
∴S=
| 1 |
| 4 |
| 1 |
| 4 |
| BC2 |
| 2 |
| (m2+1)π |
| 8 |
点评:此题考查了用待定系数法求二次函数的解析式,圆心角等于圆周角的2倍等知识点,得出∠BMC=2∠OAC=90°是解题关键.

练习册系列答案
相关题目
 (1)请你任意写5个正的真分数:
(1)请你任意写5个正的真分数: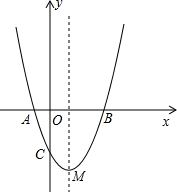 如图:已知二次函数的图象与x轴相交于点A(-1,0),B(3,0),与y轴相交于点C(0,-3).
如图:已知二次函数的图象与x轴相交于点A(-1,0),B(3,0),与y轴相交于点C(0,-3).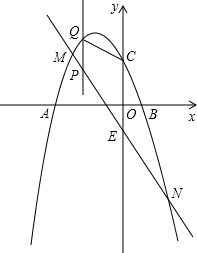 如图,抛物线y=-x2+bx+c交x轴于点A、B,交y轴于点C,其中点B坐标为(1,0),点C坐标为(0,3).
如图,抛物线y=-x2+bx+c交x轴于点A、B,交y轴于点C,其中点B坐标为(1,0),点C坐标为(0,3).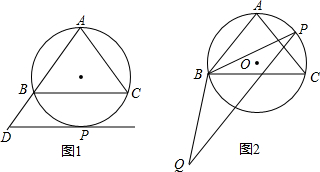

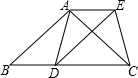 如图,在△ABC中,AB=AC,D为BC边上一点,以AB,BD为邻边?ABDE.连接AD,EC.
如图,在△ABC中,AB=AC,D为BC边上一点,以AB,BD为邻边?ABDE.连接AD,EC.