题目内容
某超市1元一双袜子进入,发现一天卖2元一双能卖500双,经过调查每升高0.1元,销量就减少10双.问定价为多少时,能达到每天的利润为800元?
考点:一元二次方程的应用
专题:销售问题
分析:设每双袜子应降价x元,根据题意列出方程,即每双袜子的利润×销售量=总盈利,再求解,把不符合题意的舍去.
解答:解:设每双袜子应定价x元,
由题意,得(x-1)(500-10×
)=800,
解得x1=3,x2=5.
答:每双袜子定价应为3或5元.
由题意,得(x-1)(500-10×
| x-2 |
| 0.1 |
解得x1=3,x2=5.
答:每双袜子定价应为3或5元.
点评:本题考查了一元二次方程的应用,解题的关键是能够从实际问题中抽象出一元二次方程模型,难度不大.

练习册系列答案
相关题目
下面是按一定规律排列的一列数:
第1个数:
-(1+
);
第2个数:
-(1+
)(1+
)(1+
);
第3个数:
-(1+
)(1+
)(1+
)(1+
)(1+
);
…
第n个数:
-(1+
)(1+
)(1+
)…(1+
).
那么,在第2011个数、第2012个数、第2013个数、第2014个数中,最大的数是( )
第1个数:
| 1 |
| 2 |
| -1 |
| 2 |
第2个数:
| 1 |
| 3 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
第3个数:
| 1 |
| 4 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
| (-1)4 |
| 5 |
| (-1)5 |
| 6 |
…
第n个数:
| 1 |
| n+1 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
| (-1)2n-1 |
| 2n |
那么,在第2011个数、第2012个数、第2013个数、第2014个数中,最大的数是( )
| A、第2011个数 |
| B、第2012个数 |
| C、第2013个数 |
| D、第2014个数 |
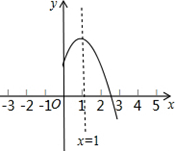 二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,其图象的一部分如图所示则①abc<0;②a-b+c<0;③3a+c<0;④当-1<x<3时,y>0.其中判断正确的有( )个.
二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,其图象的一部分如图所示则①abc<0;②a-b+c<0;③3a+c<0;④当-1<x<3时,y>0.其中判断正确的有( )个.| A、1 | B、2 | C、3 | D、4 |
时钟分针的长5cm,经过45分钟,它的针尖转过的弧长是( )
A、
| ||
B、
| ||
| C、15πcm | ||
D、
|
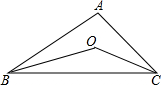 如图,O是△ABC的内心,∠BOC=100°,则∠A=
如图,O是△ABC的内心,∠BOC=100°,则∠A=