题目内容
5.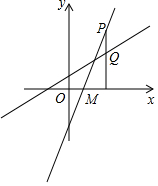 如图,点P是一次函数y=3x-2图象上的动点,过点P作直线PM⊥Ox,垂足为点M,PM交一次函数y=$\frac{2}{3}$x+1的图象于点Q,设点P的横坐标为m,当线段PQ=1时,m的值为$\frac{12}{7}$.
如图,点P是一次函数y=3x-2图象上的动点,过点P作直线PM⊥Ox,垂足为点M,PM交一次函数y=$\frac{2}{3}$x+1的图象于点Q,设点P的横坐标为m,当线段PQ=1时,m的值为$\frac{12}{7}$.
分析 根据题意得出P(m,3m-2),Q(m,$\frac{2}{3}$m+1),然后根据PQ=1,列出关于m的方程,解方程即可求得.
解答 解:设点P的横坐标为m,
∴P(m,3m-2),
∵过点P作直线PM⊥Ox,
∴Q的横坐标为m,
∵PM交一次函数y=$\frac{2}{3}$x+1的图象于点Q,
∴Q(m,$\frac{2}{3}$m+1),
∵PQ=1,
∴3m-2-($\frac{2}{3}$m+1)=1,
解得m=$\frac{12}{7}$,
故答案为$\frac{12}{7}$.
点评 本题考查了一次函数图象上点点坐标特征,根据P点横坐标和点点坐标特征求得P、Q点纵坐标上解题的关键.

练习册系列答案
相关题目
15.随着电子商务的发展,越来越多的人选择网上购物,导致各地商铺出租价格持续走低,某商业街的商铺今年1月份的出租价格为a元/平方米,2月份比1月份下降了5%,若3,4月份的出租价格按相同的百分率x继续下降,则4月份该商业街商铺的出租价格为:( )
| A. | (1-5%)a(1-2x)元 | B. | (1-5%)a(1-x)2元 | C. | (a-5%)(a-2)x元 | D. | a(1-5%-2x)元 |
14. 在Rt△ABC中,∠C=90°,BC=4,AB=5,那么sinB的值是( )
在Rt△ABC中,∠C=90°,BC=4,AB=5,那么sinB的值是( )
 在Rt△ABC中,∠C=90°,BC=4,AB=5,那么sinB的值是( )
在Rt△ABC中,∠C=90°,BC=4,AB=5,那么sinB的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
 如图,点A、C为反比例函数y=$\frac{k}{x}$(x<0)图象上的点,过点A、C分别作AB⊥x轴,CD⊥x轴,垂足分别为B、D,连接OA、AC、OC,线段OC交AB于点E,点E恰好为OC的中点,当△AEC的面积为$\frac{3}{2}$时,求k的值.
如图,点A、C为反比例函数y=$\frac{k}{x}$(x<0)图象上的点,过点A、C分别作AB⊥x轴,CD⊥x轴,垂足分别为B、D,连接OA、AC、OC,线段OC交AB于点E,点E恰好为OC的中点,当△AEC的面积为$\frac{3}{2}$时,求k的值.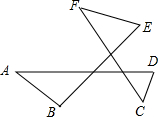 如图,∠A+∠B+∠C+∠D+∠E+∠F的和等于360度.
如图,∠A+∠B+∠C+∠D+∠E+∠F的和等于360度.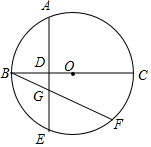 如图,BC是⊙O的直径,弦AE⊥BC,垂足为D点,$\widehat{AB}$=$\frac{1}{2}$$\widehat{BF}$,AE与BF相交于G点.
如图,BC是⊙O的直径,弦AE⊥BC,垂足为D点,$\widehat{AB}$=$\frac{1}{2}$$\widehat{BF}$,AE与BF相交于G点.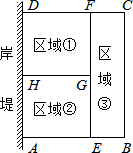 为了节省材料,某水产养殖户利用水库的岸堤(岸堤长15m)为一边,用总长为80m的栅栏围在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为y m2.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤长15m)为一边,用总长为80m的栅栏围在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为y m2. 如图,△ABC中,∠BAC=90°,D在BC上,DE⊥AB于E,DF⊥AC于F,DE=DF.
如图,△ABC中,∠BAC=90°,D在BC上,DE⊥AB于E,DF⊥AC于F,DE=DF.