题目内容
18.设x1、x2是方程x2+x-1=0的两个实数根,那么x${\;}_{1}^{3}$-2x${\;}_{2}^{2}$+2008=2006.分析 根据根与系数的关系即可得出x1+x2=-1、x1•x2=-1,结合原方程即可得出x13=2-2x12,将其代入x${\;}_{1}^{3}$-2x${\;}_{2}^{2}$+2008中即可得出结论.
解答 解:∵x1,x2是方程x2+x-1=0的两个实数根,
∴x1+x2=-1,x1•x2=-1.
又∵x13=x1x12=x1(1-x1)=x1(-x1-x2-x1)=-2x12-2x1•x2=2-2x12,
∴x13-2x22+2008=2-2x12-2x22+2008=2010-2$({x}_{1}+{x}_{2})^{2}$+2x1•x2=2010-2×(-1)2+2×(-1)=2006.
故答案为:2006.
点评 本题考查了根与系数的关系,依据根与系数的关系结合原方程找出x13=2-2x12是解题的关键.

练习册系列答案
相关题目
 如图,四边形ABDC中,∠B=∠D=90°,BC=AB,以AB为直径的⊙O交BC于E.
如图,四边形ABDC中,∠B=∠D=90°,BC=AB,以AB为直径的⊙O交BC于E.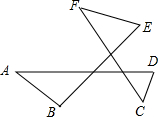 如图,∠A+∠B+∠C+∠D+∠E+∠F的和等于360度.
如图,∠A+∠B+∠C+∠D+∠E+∠F的和等于360度.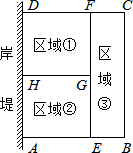 为了节省材料,某水产养殖户利用水库的岸堤(岸堤长15m)为一边,用总长为80m的栅栏围在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为y m2.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤长15m)为一边,用总长为80m的栅栏围在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为y m2. 如图,Rt△ABC中,AB=10,BC=6,E是AC上一点,AE=5,ED⊥AB,垂足为D,则AD的长为4.
如图,Rt△ABC中,AB=10,BC=6,E是AC上一点,AE=5,ED⊥AB,垂足为D,则AD的长为4.