题目内容
图1所示的遮阳伞,伞的外边缘是一个正八边形,伞炳垂直于水平地面,其示意图如图2.当伞收紧时,点P与点A重合;当伞慢慢撑开时,动点P由A向B移动;当点P到达点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN=6.0分米,CE=CF=18.0分米,BC=2.0分米
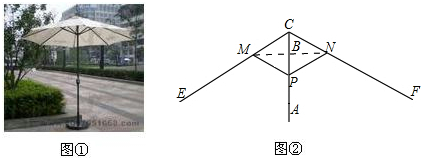
(1)当∠CPN=60°时,求AP的长度;
(2)求阳光直射下伞的阴影(正八边形)面积的最大值.(精确到0.1分米)

(1)当∠CPN=60°时,求AP的长度;
(2)求阳光直射下伞的阴影(正八边形)面积的最大值.(精确到0.1分米)
考点:相似三角形的应用
专题:
分析:(1)根据等边△PCN的判定和性质即可求解;
(2)首先求出EH2的最值,进而利用正八边形的性质求出S△HEG的值,即可得出答案.
(2)首先求出EH2的最值,进而利用正八边形的性质求出S△HEG的值,即可得出答案.
解答:解:(1)∵CN=PN,∠CPN=60°,AC=CN+PN=12分米,
∴△PCN等边三角形.
∴CP=6分米.
∴AP=AC-PC=12-6=6(分米).
即当∠CPN=60°时,AP=6分米;
(2)如图1,

连接MN,EF,分别交AC于B,H,
∵PM=PN=CM=CN,
∴四边形PNCM是菱形,
设AP=x,
∴MN与PC互相垂直平分,AC是∠ECF的平分线,
PB=
=
=6-
x,
在Rt△MBP中,PM=6分米,
故MB2=PM2-PB2=62-(6-
x)2=6x-
x2,
∵EC=CF,AC是∠ECF的平分线,
∴EH=HF,EF⊥AC,
∵∠ECFH=∠MCB,∠EHC=∠MBC=90°,
∴△CMB∽△CEH,
∴
=
,
∴
=
,
∴EH2=9MB2=9×(6x-
x2)=-
(x-12)2+324,
∵BC=2,AC=12,
∴AP最大值为10,
则EH2的最大值为:x=10时,-
(10-12)2+324=315,
如图2,

∵在正八边形中,GE=2FE=2EH•sin22.5°,FH=EH•cos22.5°,
∴S△HEG=
HF×GE
=
×2EH•sin22.5°×EH•cos22.5°
=HE2×sin45°
=
HE2,
故阳光直射下伞的阴影(正八边形)面积的最大值为:8×
HE2=8×
×315=630
≈888.3(平方分米).
∴△PCN等边三角形.
∴CP=6分米.
∴AP=AC-PC=12-6=6(分米).
即当∠CPN=60°时,AP=6分米;
(2)如图1,

连接MN,EF,分别交AC于B,H,
∵PM=PN=CM=CN,
∴四边形PNCM是菱形,
设AP=x,
∴MN与PC互相垂直平分,AC是∠ECF的平分线,
PB=
| PC |
| 2 |
| 12-x |
| 2 |
| 1 |
| 2 |
在Rt△MBP中,PM=6分米,
故MB2=PM2-PB2=62-(6-
| 1 |
| 2 |
| 1 |
| 4 |
∵EC=CF,AC是∠ECF的平分线,
∴EH=HF,EF⊥AC,
∵∠ECFH=∠MCB,∠EHC=∠MBC=90°,
∴△CMB∽△CEH,
∴
| MB |
| EH |
| CM |
| CE |
∴
| MB2 |
| EH2 |
| 1 |
| 9 |
∴EH2=9MB2=9×(6x-
| 1 |
| 4 |
| 9 |
| 4 |
∵BC=2,AC=12,
∴AP最大值为10,
则EH2的最大值为:x=10时,-
| 9 |
| 4 |
如图2,

∵在正八边形中,GE=2FE=2EH•sin22.5°,FH=EH•cos22.5°,
∴S△HEG=
| 1 |
| 2 |
=
| 1 |
| 2 |
=HE2×sin45°
=
| ||
| 4 |
故阳光直射下伞的阴影(正八边形)面积的最大值为:8×
| ||
| 4 |
| ||
| 4 |
| 2 |
点评:此题主要考查了相似三角形的性质以及正八边形的性质和锐角三角函数关系等知识,得出EH2的最大值是解题关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 有一些大小相同的小正方体组成的简单几何体,从不同方向看到的平面图形如图所示,请你猜一猜组成这个几何体的小正方体的个数.
有一些大小相同的小正方体组成的简单几何体,从不同方向看到的平面图形如图所示,请你猜一猜组成这个几何体的小正方体的个数. 如图,A、B、C、D是圆上的四点,AC=BD,求证:AD∥BC.
如图,A、B、C、D是圆上的四点,AC=BD,求证:AD∥BC. 如图所示,直线l1、l2相交于点P,试求出点P的坐标.
如图所示,直线l1、l2相交于点P,试求出点P的坐标. 如图,A、B两点在数轴上表示的数分别是a、b.
如图,A、B两点在数轴上表示的数分别是a、b.