题目内容
抛物线y=x2-mx+m2-n的顶点在直线y=2x+1上,且m-n=-2,求这条抛物线的解析式.
考点:待定系数法求二次函数解析式
专题:计算题
分析:利用顶点坐标公式表示出顶点坐标,代入y=2x+1中得到关系式,根据题意得到n=m-2,代入计算求出m与n的值,即可确定出解析式.
解答:解:由抛物线y=x2-mx+m2-n,得顶点坐标为(
,
),
∵抛物线顶点在直线y=2x+1上,
∴
=m+1,即3m2-4n=4m+4,
将n=m-2代入得:3m2-4m+8=4m+4,即3m2-8m+4=0,
分解因式得:(3m-2)(m-2)=0,
解得:m=
或m=2,
当m=
时,n=-
,此时抛物线解析式为y=x2-
x+
;
当m=2时,n=0,此时抛物线解析式为y=x2-2x+4.
| m |
| 2 |
| 3m2-4n |
| 4 |
∵抛物线顶点在直线y=2x+1上,
∴
| 3m2-4n |
| 4 |
将n=m-2代入得:3m2-4m+8=4m+4,即3m2-8m+4=0,
分解因式得:(3m-2)(m-2)=0,
解得:m=
| 2 |
| 3 |
当m=
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 16 |
| 9 |
当m=2时,n=0,此时抛物线解析式为y=x2-2x+4.
点评:此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
 如图,一段长为1500m的水渠,其截面为等腰梯形ABCD,渠深AE=0.8m,底AB=1.2m,坡角为45°,那么该水渠最多能蓄水多少立方米?
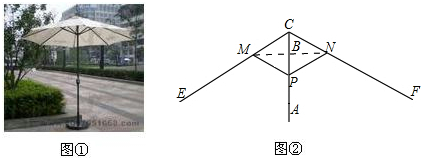
如图,一段长为1500m的水渠,其截面为等腰梯形ABCD,渠深AE=0.8m,底AB=1.2m,坡角为45°,那么该水渠最多能蓄水多少立方米? 如图,M、P分别为△ABC的边AB、AC上的点,且AM=BM,AP=2CP,BP与CM相交于N.已知PN=1,则PB的长为
如图,M、P分别为△ABC的边AB、AC上的点,且AM=BM,AP=2CP,BP与CM相交于N.已知PN=1,则PB的长为