题目内容
11.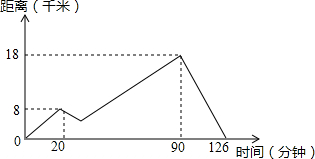 如图表示一条船从点A到河的上游点B往返的情形,从A点出发20分钟后,发动机坏了一段时间,船顺着河水倒着走了一段,之后发动机修好,继读前进到达,接着立即向点A返回.假设河水的流速、船行驶时在静水中的速度是不变的,这艘船在静水中的速度是多少?
如图表示一条船从点A到河的上游点B往返的情形,从A点出发20分钟后,发动机坏了一段时间,船顺着河水倒着走了一段,之后发动机修好,继读前进到达,接着立即向点A返回.假设河水的流速、船行驶时在静水中的速度是不变的,这艘船在静水中的速度是多少?
分析 根据①从点A出发20分钟航行的路程=船航行时间×(船在静水中速度-河水流速);②从B点返回至A点航行的路程=船返回所用时间×(船在静水中速度+河水速度);这两个等量关系列出方程组,解方程组可求出速度.
解答 解:设船行驶时在静水中的速度是x米/分钟、河水的流速是y米/分钟.则:
$\left\{\begin{array}{l}{20(x-y)=8000}\\{(126-90)(x+y)=18000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=450}\\{y=50}\end{array}\right.$.
所以这艘船在静水中的速度是450米/分钟,河水的流速是50米/分钟.
点评 本题主要考查函数图象与实际问题相结合,并抽象出方程组解决实际问题的实例,还考查解方程组的能力,属中档题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
12.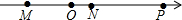 点M,N,P和原点O在数轴上的位置如图所示,点M,N,P对应的有理数为a,b,c(对应顺序暂不确定).如果ab<0,a+b>0,ac>bc,那么表示数b的点为( )
点M,N,P和原点O在数轴上的位置如图所示,点M,N,P对应的有理数为a,b,c(对应顺序暂不确定).如果ab<0,a+b>0,ac>bc,那么表示数b的点为( )
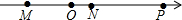 点M,N,P和原点O在数轴上的位置如图所示,点M,N,P对应的有理数为a,b,c(对应顺序暂不确定).如果ab<0,a+b>0,ac>bc,那么表示数b的点为( )
点M,N,P和原点O在数轴上的位置如图所示,点M,N,P对应的有理数为a,b,c(对应顺序暂不确定).如果ab<0,a+b>0,ac>bc,那么表示数b的点为( )| A. | 点M | B. | 点N | C. | 点P | D. | 点O |
9. 如图所示,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,下列结论:①∠BAE=30°;②CE2=AB•CF;③CF=FD;④△ABE∽△AEF.其中正确的有( )
如图所示,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,下列结论:①∠BAE=30°;②CE2=AB•CF;③CF=FD;④△ABE∽△AEF.其中正确的有( )
 如图所示,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,下列结论:①∠BAE=30°;②CE2=AB•CF;③CF=FD;④△ABE∽△AEF.其中正确的有( )
如图所示,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,下列结论:①∠BAE=30°;②CE2=AB•CF;③CF=FD;④△ABE∽△AEF.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6. 某蔬菜基地要把一批新鲜蔬菜运往外地,有两种运输方式可供选择,主要参看数据如下:
某蔬菜基地要把一批新鲜蔬菜运往外地,有两种运输方式可供选择,主要参看数据如下:
汽车、火车运输的总费用y1(元)、y2(元)与运输路程x(km)之间的函数关系的图象如图所示,结合图象解答下列问题:
(1)求m,n及y1,y2的表达式;
(2)考虑到运用汽车运输方便,只有汽车途中用时比火车的途中用时多用2小时以上(含2小时),才选用火车运输,问此时运用火车运输比用汽车运输至少节省多少元?
 某蔬菜基地要把一批新鲜蔬菜运往外地,有两种运输方式可供选择,主要参看数据如下:
某蔬菜基地要把一批新鲜蔬菜运往外地,有两种运输方式可供选择,主要参看数据如下:| 运输方式 | 运输速度(km/h) | 装卸费用(元) | 途中综合费用(元/h) |
| 汽车 | m | 200 | 270 |
| 火车 | 100 | n | 240 |
(1)求m,n及y1,y2的表达式;
(2)考虑到运用汽车运输方便,只有汽车途中用时比火车的途中用时多用2小时以上(含2小时),才选用火车运输,问此时运用火车运输比用汽车运输至少节省多少元?
3.已知点P1(1,3),点P2与点P1关于x轴对称,则P2的坐标是( )
| A. | (-5,-3) | B. | (1,-3) | C. | (-1,-3) | D. | (5,-3) |
1.用火柴棒按如图方式搭图形,按照这种方式搭下去,搭第8个图形需火柴棒的根数是( )


| A. | 48根 | B. | 50根 | C. | 52根 | D. | 54根 |
 如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=18,则S1-S2的值为3.
如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=18,则S1-S2的值为3. 如图,已知∠EAC是△ABC的外角,AD平分∠EAC,AB=AC.求证:AD∥BC.
如图,已知∠EAC是△ABC的外角,AD平分∠EAC,AB=AC.求证:AD∥BC.