题目内容

11．如图，D，E分别是△ABC边AB，BC上的点，AD=2BD，BE=CE，设△ADF的面积为S1，△CEF的面积为S2，若S△ABC=18，则S1-S2的值为3．

分析 S△ADF-S△CEF=S△ABE-S△BCD，所以求出△ABE的面积和△BCD的面积即可，因为AD=2BD，BE=CE，且S△ABC=12，就可以求出△ABE的面积和△BCD的面积．

解答 解：∵BE=CE，
∴BE=$\frac{1}{2}$BC，
∵S△ABC=18，
∴S△ABE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×18=9．
∵AD=2BD，S△ABC=18，
∴S△BCD=$\frac{1}{3}$S△ABC=6，
∵S△ABE-S△BCD=（S△ADF+S四边形BEFD）-（S△CEF+S四边形BEFD）=S△ADF-S△CEF，
即S△ADF-S△CEF=S△ABE-S△BCD=9-6=3．
故答案为3．

点评 本题考查三角形的面积，关键知道当高相等时，面积等于底边的比，据此可求出三角形的面积，然后求出差．

练习册系列答案
相关题目
1．9的算术平方根是3；3的算术平方根是$\sqrt{3}$；-1的立方根是-1；$\sqrt{2}$的相反数是-$\sqrt{2}$，倒数是$\frac{1}{\sqrt{2}}$；-$\root{3}{6}$的绝对值是$\root{3}{6}$．
2．比较大小：$\sqrt{3}$-2＜2-$\sqrt{3}$．
19．在多项式ax5+bx3+cx-3中，当x=3时，多项式的值为5，求当x=-3时多项式的值．
6．在$-\sqrt{4}$，3.14，0.3131131113…（两个“3”之间依次多一个“1”），π，$\sqrt{10}$，1.$\stackrel{•}{5}\stackrel{•}{1}$，$\frac{2}{7}$中无理数的个数有（　　）
A．1个B．2个C．3个D．4个
16．若a＜0，b＞0，且|a|＞|b|，则不正确的是（　　）
A．ab＜0B．$\frac{a}{b}$＜0C．a+b＞0D．a-b＜0
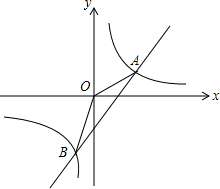3．如图：一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A（2，m）、B（-1，-4）两点．
（1）求反比例函数和一次函数的解析式；
（2）求△AOB的面积；
（3）根据图象直接写出，当x为何值时，ax+b＞$\frac{k}{x}$．
20．计算：-14+0.5$÷（-\frac{1}{2}）$2×[-3+（-1）2015]．
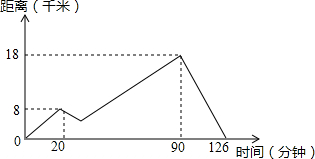11．如图表示一条船从点A到河的上游点B往返的情形，从A点出发20分钟后，发动机坏了一段时间，船顺着河水倒着走了一段，之后发动机修好，继读前进到达，接着立即向点A返回．假设河水的流速、船行驶时在静水中的速度是不变的，这艘船在静水中的速度是多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网