题目内容
如图,Rt△AB ¢C ¢ 是由Rt△ABC绕点A顺时针旋转得到的,连结CC ¢ 交斜边于点E,CC ¢ 的延长线交BB ¢ 于点F.
(1)证明:△ACE∽△FBE;
(2)设∠ABC=![]() ,∠CAC¢ =
,∠CAC¢ =![]() ,试探索
,试探索![]() 、
、![]() 满足什么关系时,△ACE与△FBE是全等三角形,并说明理由.
满足什么关系时,△ACE与△FBE是全等三角形,并说明理由.
(1)略
(2)是,理由略
解析:(1)证明:∵Rt△AB ¢C ¢ 是由Rt△ABC绕点A顺时针旋转得到的,
∴AC=AC ¢,AB=AB ¢,∠CAB=∠C ¢AB ¢ ………………(1分)
∴∠CAC ¢=∠BAB ¢
∴∠ACC ¢=∠ABB ¢ ……………………………………(3分)
又∠AEC=∠FEB
∴△ACE∽△FBE ……………………………………(4分)
(2)解:当![]() 时,△ACE≌△FBE. …………………(5分)
时,△ACE≌△FBE. …………………(5分)
在△ACC¢中,∵AC=AC ¢,
∴![]() ………(6分)
………(6分)
在Rt△ABC中,
∠ACC¢+∠BCE=90°,即![]() ,
,
∴∠BCE=![]() .
.
∵∠ABC=![]() ,
,
∴∠ABC=∠BCE ……………………(8分)
∴CE=BE
由(1)知:△ACE∽△FBE,
∴△ACE≌△FBE.………………………(9分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
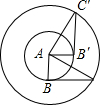 如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=1,BC=2,则旋转过程中弧CC′的长为( )
如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=1,BC=2,则旋转过程中弧CC′的长为( )A、
| ||||
B、
| ||||
| C、5π | ||||
D、
|
 如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F.证明:
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F.证明: 如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F.
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F.
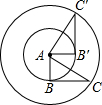 如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=1,BC=2,则旋转过程中
如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=1,BC=2,则旋转过程中