题目内容
 如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F.
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F.(1)证明:∠ACE=∠FBE;
(2)设∠ABC=α,∠CAC′=β,若△ACE≌△FBE,试探索α、β满足什么关系?并说明理由.
分析:(1)根据旋转的性质可得AC=AC′,AB=AB′,∠CAC′=∠BAB′,然后根据等腰三角形两底角相等列式整理即可得证;
(2)根据全等三角形对应边相等可得BE=CE,根据等边对等角可得∠ABC=∠BCE,再根据∠ACB=∠BCE+∠ACC′=90°代入整理数据整理即可得解.
(2)根据全等三角形对应边相等可得BE=CE,根据等边对等角可得∠ABC=∠BCE,再根据∠ACB=∠BCE+∠ACC′=90°代入整理数据整理即可得解.
解答:(1)证明:∵Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到,
∴AC=AC′,AB=AB′,∠CAC′=∠BAB′,
∴∠ACE=
(180°-∠CAC′),∠FBE=
(180°-∠BAB′),
∴∠ACE=∠FBE;
(2)解:∵△ACE≌△FBE,
∴BE=CE,
∴∠ABC=∠BCE=α,
∵∠CAC′=β,AC=AC′,
∴∠ACE=
(180°-∠CAC′)=
(180°-β),
∵∠ACB=∠BCE+∠ACC′=90°,
∴α+
(180°-β)=90°,
整理得,β=2α.
∴AC=AC′,AB=AB′,∠CAC′=∠BAB′,
∴∠ACE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ACE=∠FBE;
(2)解:∵△ACE≌△FBE,
∴BE=CE,
∴∠ABC=∠BCE=α,
∵∠CAC′=β,AC=AC′,
∴∠ACE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ACB=∠BCE+∠ACC′=90°,
∴α+
| 1 |
| 2 |
整理得,β=2α.
点评:本题考查了旋转的性质,全等三角形的性质,等腰三角形等边对等角的性质,熟练掌握各图形的性质是解题的关键.

练习册系列答案
相关题目
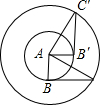 如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=1,BC=2,则旋转过程中弧CC′的长为( )
如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=1,BC=2,则旋转过程中弧CC′的长为( )A、
| ||||
B、
| ||||
| C、5π | ||||
D、
|
 如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F.证明:
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F.证明:
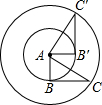 如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=1,BC=2,则旋转过程中
如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其中AB=1,BC=2,则旋转过程中