题目内容
16. 如图,DE∥BC,若S△ADE:S△ABC=4:25,AD=4,则BD的值为( )
如图,DE∥BC,若S△ADE:S△ABC=4:25,AD=4,则BD的值为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 根据DE∥BC,得到△ADE∽△ABC,由相似三角形的性质得到S△ADE:S△ABC=($\frac{AD}{AB}$)2=4:25,求得AD:AB=2:5,得到AB=10,于是得到结论.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∴S△ADE:S△ABC=($\frac{AD}{AB}$)2=4:25,
∴AD:AB=2:5,
∵AD=4,
∴AB=10,
∴BD=AB-AD=6,
故选B.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
6.$\sqrt{(-4)^{2}}$的平方根是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±4 |
8.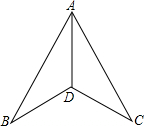 如图,在下列条件中,不能证明△ABD≌△ACD的是( )
如图,在下列条件中,不能证明△ABD≌△ACD的是( )
 如图,在下列条件中,不能证明△ABD≌△ACD的是( )
如图,在下列条件中,不能证明△ABD≌△ACD的是( )| A. | BD=DC,AB=AC | B. | ∠ADB=∠ADC,AB=AC | C. | ∠B=∠C,∠BAD=∠CAD | D. | ∠ADB=∠ADC,BD=CD |
5. 如图,两块直角三角板的直顶角O重合在一起,若∠BOC=$\frac{1}{5}$∠AOD,则∠BOC的度数为( )
如图,两块直角三角板的直顶角O重合在一起,若∠BOC=$\frac{1}{5}$∠AOD,则∠BOC的度数为( )
 如图,两块直角三角板的直顶角O重合在一起,若∠BOC=$\frac{1}{5}$∠AOD,则∠BOC的度数为( )
如图,两块直角三角板的直顶角O重合在一起,若∠BOC=$\frac{1}{5}$∠AOD,则∠BOC的度数为( )| A. | 30° | B. | 45° | C. | 54° | D. | 60° |
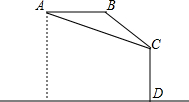 如图,热气球在离地面800米的A处,在A处测得一大楼顶C的俯角是30°,热气球沿着水平方向向此大楼飞行400米后达到B处,从B处再次测得此大楼楼顶C的俯角是45°,求该大楼CD的高度.
如图,热气球在离地面800米的A处,在A处测得一大楼顶C的俯角是30°,热气球沿着水平方向向此大楼飞行400米后达到B处,从B处再次测得此大楼楼顶C的俯角是45°,求该大楼CD的高度. 如图,在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=$\frac{1}{2}$BD,DF⊥AB于F.求证:CD=DF.
如图,在△ABC中,∠C=90°,AC=BC,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=$\frac{1}{2}$BD,DF⊥AB于F.求证:CD=DF.