题目内容
5.解方程:(1)$\frac{2}{x-1}=\frac{4}{{x}^{2}-1}$;
(2)$\frac{2-x}{x-3}+\frac{1}{3-x}$=1.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:2x+2=4,
解得:x=1,
经检验x=1是增根,分式方程无解;
(2)去分母得:2-x-1=x-3,
解得:x=2,
经检验x=2是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
15.下列各组图形中,一定相似的是( )
| A. | 任意两个矩形 | B. | 任意两个菱形 | ||
| C. | 任意两个直角三角形 | D. | 任意两个等边三角形 |
14.计算${({-2})^2}+|{-3}|×\frac{1}{3}$的结果为( )
| A. | -5 | B. | 5 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
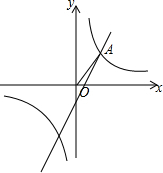 如图,已知反比例函数y=$\frac{k}{2x}$和一次函数y=2x-1,其中一次函数的图象经过M(a,b),N(a+1,b+k)两点.
如图,已知反比例函数y=$\frac{k}{2x}$和一次函数y=2x-1,其中一次函数的图象经过M(a,b),N(a+1,b+k)两点.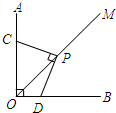 已知:∠AOB=∠CPD=90°,OM是∠AOB的平分线,求证:PC=PD.
已知:∠AOB=∠CPD=90°,OM是∠AOB的平分线,求证:PC=PD.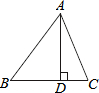 如图所示,在△ABC中,AD是BC边上的高,AB=15,AC=13,AD=12,根据上述数据,你能求得△ABC的面积吗?试试看.
如图所示,在△ABC中,AD是BC边上的高,AB=15,AC=13,AD=12,根据上述数据,你能求得△ABC的面积吗?试试看.