题目内容
20.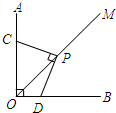 已知:∠AOB=∠CPD=90°,OM是∠AOB的平分线,求证:PC=PD.
已知:∠AOB=∠CPD=90°,OM是∠AOB的平分线,求证:PC=PD.
分析 过点P点作PE⊥OA于E,PF⊥OB于F,根据垂直的定义得到∠PEC=∠PFD=90°,由OM是∠AOB的平分线,根据角平分线的性质得到PE=PF,利用四边形内角和定理可得到∠PCE+∠PDO=360°-90°-90°=180°,而∠PDO+∠PDF=180°,则∠PCE=∠PDF,然后根据“AAS”可判断△PCE≌△PDF,根据全等的性质即可得到PC=PD.
解答 解:如图,过点P点作PE⊥OA于E,PF⊥OB于F,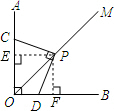
∴∠PEC=∠PFD=90°,
∵OM是∠AOB的平分线,
∴PE=PF,
∵∠AOB=90°,∠CPD=90°,
∴∠PCE+∠PDO=360°-90°-90°=180°,
而∠PDO+∠PDF=180°,
∴∠PCE=∠PDF,
在△PCE和△PDF中,
$\left\{\begin{array}{l}{∠PCE=∠PDF}\\{∠PEC=∠PFD}\\{PE=PF}\end{array}\right.$
∴△PCE≌△PDF(AAS),
∴PC=PD.
点评 本题考查了角平分线的性质:角平分线上的点到这个角两边的距离相等,考查了三角形全等的判定与性质.解决本题的关键是熟记角平分线的性质,全等三角形的性质与判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列各式中计算错误的是( )
| A. | 2x(2x3+3x-1)=4x4+6x2-2x | B. | b(b2-b+1)=b3-b2+b | ||
| C. | -$\frac{1}{2}x(2{x^2}-2)=-{x^3}$-x | D. | $\frac{2}{3}x(\frac{3}{2}{x^3}-3x+1)={x^4}-2{x^2}+\frac{2}{3}$x |
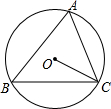 如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为18°.
如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为18°.