题目内容
9.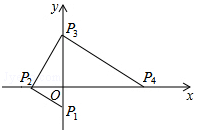 如图,点P1,P2,P3,P4均在坐标轴上,且P1P2⊥P2P3,P2P3⊥P3P4,若点P1,P2的坐标分别为(0,-1),(-2,0),求点P4的坐标.
如图,点P1,P2,P3,P4均在坐标轴上,且P1P2⊥P2P3,P2P3⊥P3P4,若点P1,P2的坐标分别为(0,-1),(-2,0),求点P4的坐标.
分析 根据相似三角形的性质求出P3D的坐标,再根据相似三角形的性质计算求出OP4的长,得到答案.
解答 解:∵点P1,P2的坐标分别为(0,-1),(-2,0),
∴OP1=1,OP2=2,
∵Rt△P1OP2∽Rt△P2OP3,
∴$\frac{O{P}_{1}}{O{P}_{2}}$=$\frac{O{P}_{2}}{O{P}_{3}}$,即$\frac{1}{2}$=$\frac{2}{O{P}_{3}}$,
解得,OP3=4,
∵Rt△P2OP3∽Rt△P3OP4,
∴$\frac{O{P}_{2}}{O{P}_{3}}$=$\frac{O{P}_{3}}{O{P}_{4}}$,即$\frac{2}{4}$=$\frac{4}{O{P}_{4}}$,
解得,OP4=8,
则点P4的坐标为(8,0).
点评 本题考查的是相似三角形的判定和性质以及坐标与图形的性质,掌握相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
4.把二次函数y=x2-2x+3配方成y=(x-m)2+k的形式,以下结果正确的是( )
| A. | y=-(x-1)2+4 | B. | y=(x-1)2+2 | C. | y=(x+1)2+2 | D. | y=(x-2)2+3 |
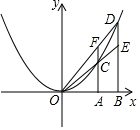 如图,在x轴上有两点A(m,0),B(n,0)(n>m>0),分别过点A,点B作x轴的垂线,交抛物线y=x2于点C,点D.直线OC交直线BD于点E,直线OD交直线AC于点F,点E,点F的纵坐标分别记作yE,yF
如图,在x轴上有两点A(m,0),B(n,0)(n>m>0),分别过点A,点B作x轴的垂线,交抛物线y=x2于点C,点D.直线OC交直线BD于点E,直线OD交直线AC于点F,点E,点F的纵坐标分别记作yE,yF