题目内容
18.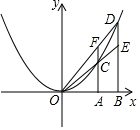 如图,在x轴上有两点A(m,0),B(n,0)(n>m>0),分别过点A,点B作x轴的垂线,交抛物线y=x2于点C,点D.直线OC交直线BD于点E,直线OD交直线AC于点F,点E,点F的纵坐标分别记作yE,yF
如图,在x轴上有两点A(m,0),B(n,0)(n>m>0),分别过点A,点B作x轴的垂线,交抛物线y=x2于点C,点D.直线OC交直线BD于点E,直线OD交直线AC于点F,点E,点F的纵坐标分别记作yE,yF(1)特例探究
当m=1,n=2时,yE=2,yF=2
当m=3,n=5时,yE=15,yF=15
(2)归纳证明
对任意m,n(n>m>0),猜想yE与yF的大小关系,并证明你的猜想.
(3)拓展应用
若将抛物线y=x2改为抛物线y=ax2(a>0),其它条件不变,请直接写出yE与yF的大小关系.
分析 (1)已知A、B的坐标,根据抛物线的解析式,能得到C、D的坐标,进而能求出直线OC、OD的解析式,也就能得出E、F两点的坐标,再进行比较即可.
(2)已知A、B的坐标,根据抛物线的解析式,能得到C、D的坐标,进而能求出直线OC、OD的解析式,也就能得出E、F两点的坐标,再进行比较即可.
(3)已知A、B的坐标,根据抛物线的解析式,能得到C、D的坐标,进而能求出直线OC、OD的解析式,也就能得出E、F两点的坐标,再进行比较即可.
解答 解:(1)特例探究:
当m=1,n=2时,A(1,0)、B(2,0)、C(1,1)、D(2,4);
则:直线OC:y=x;直线OD:y=2x;
∴F(1,2)、E(2,2);
即:yE=yF=2.
同理:当m=3,n=5时,yE=yF=15.
故答案为2,2;15,15;
(2)归纳证明:
猜想:yE=yF;
证明:点A(m,0),B(n,0)(n>m>0).
由抛物线的解析式知:C(m,m2)、D(n,n2);
设直线OC的解析式:y=kx,代入点C的坐标:
km=m2,k=m
即:直线OC:y=mx;
同理:直线OD:y=nx.
∴E(n,mn)、F(m,mn)
即yE=yF.
(3)拓展应用:yE=yF.
证明:点A(m,0),B(n,0)(n>m>0).
由抛物线的解析式知:C(m,am2)、D(n,an2);
设直线OC的解析式:y=kx,代入点C的坐标:
km=am2,k=am
即:直线OC:y=amx;
同理:直线OD:y=anx.
∴E(n,amn)、F(m,amn)
即yE=yF.
点评 本题主要考查的是二次函数图象是点的坐标特征,表示出E、F点的坐标是解题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
8.下列调查中,最适合采用普查方式的是( )
| A. | 对重庆市石柱县中小学视力情况的调查 | |
| B. | 对动车重要零部件的调查 | |
| C. | 对市场上方便面质量的调查 | |
| D. | 对重庆市“雾都夜话”栏目收视率的调查 |
3.下列图形中,既是轴对称图形又是中心对称是( )
| A. |  | B. |  | C. |  | D. |  |
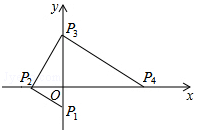 如图,点P1,P2,P3,P4均在坐标轴上,且P1P2⊥P2P3,P2P3⊥P3P4,若点P1,P2的坐标分别为(0,-1),(-2,0),求点P4的坐标.
如图,点P1,P2,P3,P4均在坐标轴上,且P1P2⊥P2P3,P2P3⊥P3P4,若点P1,P2的坐标分别为(0,-1),(-2,0),求点P4的坐标. 若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.
若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”.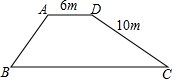 如图是一座堤坝的横断面,AB坡坡角为45°,DC坡坡度为1:2,其他数据如图所示,求BC的长(精确到0.1m).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{5}$≈2.236)
如图是一座堤坝的横断面,AB坡坡角为45°,DC坡坡度为1:2,其他数据如图所示,求BC的长(精确到0.1m).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{5}$≈2.236)