题目内容
15.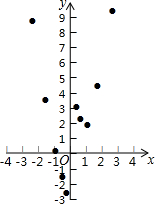 根据学习函数的经验,小明对函数y=x2+$\frac{1}{x}$的图象与性质进行了探究.下面是小明的探究过程,请补充完成:
根据学习函数的经验,小明对函数y=x2+$\frac{1}{x}$的图象与性质进行了探究.下面是小明的探究过程,请补充完成:(1)函数y=x2+$\frac{1}{x}$的自变量x的取值范围是x≠0.
(2)下表是y与x的几组对应值,其中m=$\frac{28}{3}$;
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | $\frac{26}{3}$ | $\frac{7}{2}$ | 0 | -$\frac{7}{4}$ | -$\frac{26}{9}$ | $\frac{28}{9}$ | $\frac{9}{4}$ | 2 | $\frac{9}{2}$ | m | … |
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,2),结合函数的图象,写出该函数的其它性质(一条即可)该函数没有最大值或该函数没有最小值或该函数不经过第四象限或该函数在x=0处断开..
分析 (1)根据分母不能为零即可写出x的取值范围.
(2)x=3代入解析式计算即可求出m.
(3)描点法画图即可.
(4)根据图象写一条符合该函数图象的性质即可.
解答 解;(1)函数y=x2+$\frac{1}{x}$的自变量x的取值范围是x≠0.
故答案为x≠0;
(2)x=3时,m=32+$\frac{1}{3}$=$\frac{28}{3}$.
故答案为$\frac{28}{3}$;
(3)该函数图象如图所示,
(4)该函数没有最大值或该函数没有最小值或该函数不经过第四象限或该函数在x=0处断开.
故答案为:该函数没有最大值或该函数没有最小值或该函数不经过第四象限或该函数在x=0处断开.
点评 本题考查函数的图象的性质,会用描点法画出函数图象,利用数形结合的思想写出函数的性质,是一条开放性题目,难度不大.

练习册系列答案
相关题目
6.用给定长度的绳子围成下面四种几何图形,其面积一定最大的是( )
| A. | 三角形 | B. | 平行四边形 | C. | 正方形 | D. | 菱形 |
7.下列各组式子中,为同类项的是( )
| A. | 5x2y与-2xy2 | B. | 3x与3x2 | C. | -2xy与5yx | D. | 4a2b与3a2c |
4.下列运算正确的是( )
| A. | a3÷a=a3(a≠0) | B. | (-a)4=a4 | C. | 3a2•2a2=6a2 | D. | (a-b)2=a2-b2 |
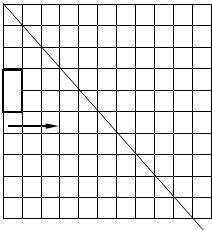 如图,矩形ABCD是一颗水平向右匀速飞行的“卫星”,直线l1是一束高能射线
如图,矩形ABCD是一颗水平向右匀速飞行的“卫星”,直线l1是一束高能射线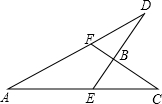 如图,已知∠CBE=96°,∠A=27°,∠C=30°,则∠ADE=27°.
如图,已知∠CBE=96°,∠A=27°,∠C=30°,则∠ADE=27°.