题目内容
4.下列运算正确的是( )| A. | a3÷a=a3(a≠0) | B. | (-a)4=a4 | C. | 3a2•2a2=6a2 | D. | (a-b)2=a2-b2 |
分析 根据同底数幂的除法、乘法,完全平方公式,即可解答.
解答 解:A、a3÷a=a2(a≠0),故错误;
B、(-a)4=a4,正确;
C、3a2•2a2=6a4,故错误;
D、(a-b)2=a2-2ab+b2,故错误;
故选:B.
点评 本题考查了同底数幂的除法、乘法,完全平方公式,解决本题的关键是熟记同底数幂的除法、乘法,完全平方公式.

练习册系列答案
相关题目
15.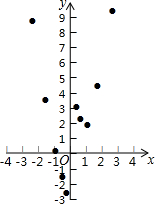 根据学习函数的经验,小明对函数y=x2+$\frac{1}{x}$的图象与性质进行了探究.下面是小明的探究过程,请补充完成:
根据学习函数的经验,小明对函数y=x2+$\frac{1}{x}$的图象与性质进行了探究.下面是小明的探究过程,请补充完成:
(1)函数y=x2+$\frac{1}{x}$的自变量x的取值范围是x≠0.
(2)下表是y与x的几组对应值,其中m=$\frac{28}{3}$;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,2),结合函数的图象,写出该函数的其它性质(一条即可)该函数没有最大值或该函数没有最小值或该函数不经过第四象限或该函数在x=0处断开..
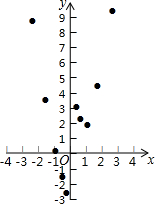 根据学习函数的经验,小明对函数y=x2+$\frac{1}{x}$的图象与性质进行了探究.下面是小明的探究过程,请补充完成:
根据学习函数的经验,小明对函数y=x2+$\frac{1}{x}$的图象与性质进行了探究.下面是小明的探究过程,请补充完成:(1)函数y=x2+$\frac{1}{x}$的自变量x的取值范围是x≠0.
(2)下表是y与x的几组对应值,其中m=$\frac{28}{3}$;
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | $\frac{26}{3}$ | $\frac{7}{2}$ | 0 | -$\frac{7}{4}$ | -$\frac{26}{9}$ | $\frac{28}{9}$ | $\frac{9}{4}$ | 2 | $\frac{9}{2}$ | m | … |
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,2),结合函数的图象,写出该函数的其它性质(一条即可)该函数没有最大值或该函数没有最小值或该函数不经过第四象限或该函数在x=0处断开..
9.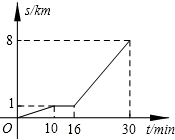 成都市二环路高架环线快速公交已开通,小彬从家步行到公交车站台,等公交车去学校.图中的折线表示小彬的行程s (千米)与所花时间t (分钟)之间的函数关系,下列说法错误的是( )
成都市二环路高架环线快速公交已开通,小彬从家步行到公交车站台,等公交车去学校.图中的折线表示小彬的行程s (千米)与所花时间t (分钟)之间的函数关系,下列说法错误的是( )
 成都市二环路高架环线快速公交已开通,小彬从家步行到公交车站台,等公交车去学校.图中的折线表示小彬的行程s (千米)与所花时间t (分钟)之间的函数关系,下列说法错误的是( )
成都市二环路高架环线快速公交已开通,小彬从家步行到公交车站台,等公交车去学校.图中的折线表示小彬的行程s (千米)与所花时间t (分钟)之间的函数关系,下列说法错误的是( )| A. | 他离家8千米,共用了30分钟 | B. | 他等公交车时间为6分钟 | ||
| C. | 他步行的速度是100米/分钟 | D. | 公交车的速度是350米/分钟 |
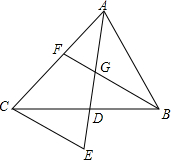 如图:△ABC中,AD,BF为中线,AD,BF相交于G,CE∥FB交AD的延长线于E,AG=6cm,求DE的长.
如图:△ABC中,AD,BF为中线,AD,BF相交于G,CE∥FB交AD的延长线于E,AG=6cm,求DE的长.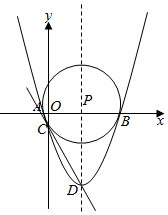 如图,已知二次函数y=$\frac{1}{3}$x2-$\frac{8}{3}$x-3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为(4,0)或(4,$\frac{75}{8}$).
如图,已知二次函数y=$\frac{1}{3}$x2-$\frac{8}{3}$x-3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为(4,0)或(4,$\frac{75}{8}$).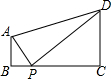 如图,AB⊥BC,DC⊥BC,AB=1,DC=2,BC=3,点P是线段BC上一动点(不与点B、C重合),若△APD是等腰三角形,则CP的长是1或$\sqrt{6}$.
如图,AB⊥BC,DC⊥BC,AB=1,DC=2,BC=3,点P是线段BC上一动点(不与点B、C重合),若△APD是等腰三角形,则CP的长是1或$\sqrt{6}$.