题目内容
18.已知分式$\frac{2x-m}{x+n}$,当x=3时,分式的值不存在;当x=-1时,分式的值等于0.求$\frac{{{m}^{2}+n}^{2}}{m-n}$的值.分析 先根据分式的值为0的条件求出n的值,再由当x=-1时,分式的值等于0求出m的值,代入代数式进行计算即可.
解答 解:∵当x=3时,分式的值不存在,
∴3+n=0,解得n=-3;
∵当x=-1时,分式的值等于0,
∴-2-m=0,解得m=-2,
∴原式=$\frac{{{(-2)}^{2}+3}^{2}}{-2+3}$=13.
点评 本题考查的是分式有意义的条件,熟知分式有意义的条件是分母不等于零是解答此题的关键.

练习册系列答案
相关题目
10.若$\frac{a}{b}>0$,$\frac{c}{b}<0$,则ac( )
| A. | 大于0 | B. | 小于0 | C. | 不一定 | D. | 等于0 |
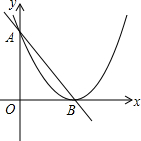 如图,直线y=-x+3交x轴于点B,交y轴于点A.抛物线的顶点为点B,且经过点A.
如图,直线y=-x+3交x轴于点B,交y轴于点A.抛物线的顶点为点B,且经过点A. 如图是举世闻名的三星堆考古中挖掘出的一个三角形残缺玉片,工作人员想制作该玉片模型,则测量图中哪些数据,就可制成符合规格的三角形玉片模型?请说明其中的道理.
如图是举世闻名的三星堆考古中挖掘出的一个三角形残缺玉片,工作人员想制作该玉片模型,则测量图中哪些数据,就可制成符合规格的三角形玉片模型?请说明其中的道理.