题目内容
6.解下列方程:(1)x2-6x-5=0;
(2)(2x-3)2=(x+1)2.
分析 (1)利用配方法解方程即可;
(2)利用平方差公式因式分解求得方程的解即可.
解答 解:(1)x2-6x-5=0,
x2-6x+9=5+9,
(x-3)2=14,
x-3=±$\sqrt{14}$,
x1=3+$\sqrt{14}$,x2=3-$\sqrt{14}$;
(2)(2x-3)2=(x+1)2,
(2x-3)2-(x+1)2=0,
(2x-3+x+1)(2x-3-x-1)=0,
(3x-2)(x-4)=0,
x1=$\frac{2}{3}$,x2=4.
点评 此题考查用因式分解法和配方法解一元二次方程,掌握解方程的步骤与方法,根据方程的不同特点选择合适的方法是解决问题的关键.

练习册系列答案
相关题目
16.下列方程:①$\frac{1}{x}$=2;②$\frac{x-1}{3}$=$\frac{x}{2}$;③$\frac{x}{5}$+x=1;④$\frac{2}{x-1}$+$\frac{3}{1-x}$=3.其中,分式方程有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
16.运用乘法法则将右表填写完整.
| × | -2 | $-\frac{3}{4}$ | 1$\frac{1}{2}$ | 0 |
| 3 | -6 | -$\frac{9}{4}$ | 4 | 0 |
| -8 | 16 | 6 | -12 | 0 |
| $-\frac{2}{3}$ | $\frac{4}{3}$ | $\frac{1}{2}$ | -1 | 0 |
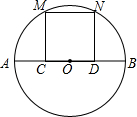 如图所示,在⊙O中,C、D分别是OA、OB的中点,MC⊥AB、ND⊥AB,M、N在⊙O上.
如图所示,在⊙O中,C、D分别是OA、OB的中点,MC⊥AB、ND⊥AB,M、N在⊙O上.