Question

1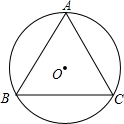．如图，△ABC内接于⊙O，
（1）作弦BC的弦心距OD（要求：用尺规作图，保留作图痕迹）；
（2）若∠A=60°，AB=AC=2，求OD的长．

Answer 1

分析 （1）过点O作OD⊥BC于D，则OD为弦BC的弦心距；
（2）连结OB、OC，如图，先判断△ABC为等边三角形，则BC=AB=2，根据垂径定理得BD=CD=1，根据圆周角定理得∠BOC=2∠A=120°，则根据三角形内角和可计算出∠OBC=30°，然后在Rt△OBD中利用正切定理可计算出OD的长．

解答 解：（1）如图，OD为所作；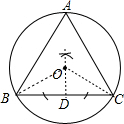

（2）连结OB、OC，如图，
∵∠A=60°，AB=AC=2，
∴△ABC为等边三角形，
∴BC=AB=2，
∵OD⊥BC，
∴BD=CD=1，
∵∠BOC=2∠A=120°，
∴∠OBC=$\frac{1}{2}$（180°-120°）=30°，
在Rt△OBD中，∵tan∠OBD=$\frac{OD}{BD}$，
∴OD=1×tan30°=$\frac{\sqrt{3}}{3}$．

点评 本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了三角形的外心．