题目内容
4. (1)请作出△ABC中AC边上的高BD;
(1)请作出△ABC中AC边上的高BD;(2)作出△ABC中线CG.
分析 (1)以B为圆心,适当的长为半径画弧,交AC于M,N两点,分别以M,N为圆心,适当的长的半径画弧,两弧交于点E,作射线BE,交AC于D,则BD是△ABC中AC边上的高;
(2)分别以A,B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧交于点F,H,作直线FH,交AB于G,连接CG,则CG是△ABC的中线.
解答 解:(1)如图所示,线段BD即为所求;
(2)如图所示,线段CG即为所求.
点评 本题主要考查了利用作垂线和作垂直平分线两种基本作图进行复杂作图,解决问题的关键是掌握作已知线段的垂直平分线和过一点作已知直线的垂线的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.设a=2°,b=(-3)2,c=$\root{3}{27}$,d=($\frac{1}{2}$) -1,则a、b、c、d按由小到大的顺序排列正确的是( )
| A. | a<d<c<b | B. | a<b<c<d | C. | d<a<c<b | D. | b<d<c<a |
14.下列语句中,正确的是( )
| A. | 若∠α+∠β=180°,则∠α是补角 | |
| B. | 若∠AOB+∠BOC=180°,则∠AOC是直角 | |
| C. | 若∠α与∠β互为补角,则∠α与∠β中必有一个为锐角,另一个角为钝角 | |
| D. | 若∠α与∠β互为余角,则∠α+∠β=90° |
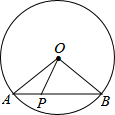 如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是60°或120°.
如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是60°或120°.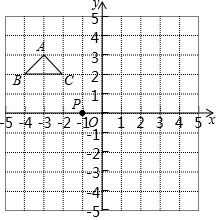 在建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,点P的坐标为(-1,0),请按要求画图与作答:
在建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,点P的坐标为(-1,0),请按要求画图与作答: 如图所示的正方形网格中一共有20个长方形.
如图所示的正方形网格中一共有20个长方形.