题目内容
9.解方程:(1)$\frac{1}{x+2}+\frac{4x}{{{x^2}-4}}=\frac{2}{x-2}$
(2)$\frac{3}{2x-2}+\frac{1}{1-x}$=3.
分析 把分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)方程两边乘以(x+2)(x-2)得:x-2+4x=2(x+2),
解得:x=2,
检验:x=2时,(x+2)(x-2)=0,x=2不是原方程的解:
因此,原方程无解.
(2)方程两边乘以2(x-1)得:3-2=6(x-1),
解得:x=$\frac{7}{6}$,
检验:x=$\frac{7}{6}$时,2(x-1)≠0,x=$\frac{7}{6}$是原方程的解:
因此,原方程的解为x=$\frac{7}{6}$.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.使$\sqrt{3x-4}$有意义的x的取值范围是( )
| A. | x>$\frac{4}{3}$ | B. | x>$\frac{3}{4}$ | C. | x$≥\frac{3}{4}$ | D. | x≥$\frac{4}{3}$ |
4.若点(3、4)在反比例函数y=$\frac{k}{x}$ (k≠0)的图象上,则该函数图象一定经过( )
| A. | (2、6) | B. | (2、-6) | C. | (4、-3) | D. | (3、-4) |
14. 有理数a,b在数轴上对应的点的位置如图所示,下列结论成立的是( )
有理数a,b在数轴上对应的点的位置如图所示,下列结论成立的是( )
 有理数a,b在数轴上对应的点的位置如图所示,下列结论成立的是( )
有理数a,b在数轴上对应的点的位置如图所示,下列结论成立的是( )| A. | a+b>0 | B. | a+b=0 | C. | a+b<0 | D. | a-b>0 |
1.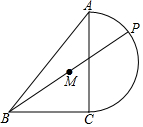 如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )
 如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )
如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )| A. | 2$\sqrt{2}$π | B. | $\sqrt{2}$π | C. | 2π | D. | 2$\sqrt{2}$ |



