题目内容
19.解方程:$\frac{2}{x+1}-1=\frac{1}{1-x}$.分析 根据等式的性质,可得整式方程,根据解整式方程,可得答案.
解答 解:方程两边都乘以(1+x)(1-x),得
x2-3x=0.
解得x1=0,x2=3,
检验:x=0时,(x+1)(1-x)≠0,
x=3时,(x+1)(1-x)≠0,
∴原分式方程的解为x1=0,x2=3.
点评 本题考查了解分式方程,利用等式的性质得出整式方程是解题关键,

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
10.下列方程中,有实数根的方程是( )
| A. | $\sqrt{x-2}+1=0$ | B. | $\frac{x}{{{x^2}-1}}=\frac{1}{{{x^2}-1}}$ | C. | x5+32=0 | D. | 2x2+x+1=0 |
8.如果a<b,那么下列结论一定成立的是( )
| A. | a+5<b+5 | B. | a-b>0 | C. | a+7>b-7 | D. | c-a<c-b |
9.若点A(a,b)在反比例函数y=$\frac{3}{x}$的图象上,则代数式ab-1的值为( )
| A. | 0 | B. | -2 | C. | 2 | D. | -6 |
 如图,平面上有四个点A、B、C、D,根据下列语句画图
如图,平面上有四个点A、B、C、D,根据下列语句画图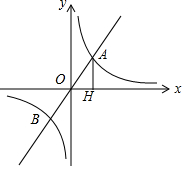 已知:如图,正比例函数y=k1x的图象与反比例函数$y=\frac{k_2}{x}$的图象相交于点A、B,点A在第一象限,且点A的横坐标为1,作AH垂直于x轴,垂足为点H,S△AOH=1.
已知:如图,正比例函数y=k1x的图象与反比例函数$y=\frac{k_2}{x}$的图象相交于点A、B,点A在第一象限,且点A的横坐标为1,作AH垂直于x轴,垂足为点H,S△AOH=1.