题目内容
 在正方形网格中,△ABC如图放置,则sinB的值为
在正方形网格中,△ABC如图放置,则sinB的值为考点:勾股定理,三角形的面积,锐角三角函数的定义
专题:网格型
分析:过D作DF⊥BC,在网格中利用勾股定理求出BD与BE的长,找出BG与DE的长,利用三角形的面积法求出DF的产,在直角三角形BDF中,利用锐角三角函数定义即可求出sinB的值.
解答: 解:过D作DF⊥BC,
解:过D作DF⊥BC,
根据勾股定理得:BD=BE=
,且DE=2,BG=2,BG⊥DE,
∵S△BDE=
DE•BG=
BE•DF,
∴DF=
=
,
在Rt△BDF中,sinB=
=
=
=0.8.
故答案为:0.8.
 解:过D作DF⊥BC,
解:过D作DF⊥BC,根据勾股定理得:BD=BE=
| 5 |
∵S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
∴DF=
| 2×2 | ||
|
4
| ||
| 5 |
在Rt△BDF中,sinB=
| DF |
| BD |
| ||||
|
| 4 |
| 5 |
故答案为:0.8.
点评:此题考查了勾股定理,三角形的面积,以及锐角三角函数定义,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
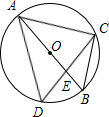 如图,AB是⊙O的直径,△ACD为正三角形,则∠BAC=
如图,AB是⊙O的直径,△ACD为正三角形,则∠BAC=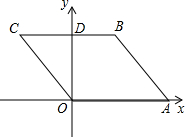 如图,菱形OABC的面积为
如图,菱形OABC的面积为 如图所示,在直角坐标系xOy中,直线L:y=-x-1,双曲线y=
如图所示,在直角坐标系xOy中,直线L:y=-x-1,双曲线y= 如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,面积记作S1;再作第二个正方形A2B2C2A3,面积记作S2;继续作第三个正方形A3B3C3A4,面积记作S3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第6个正方形的面积S6是
如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,面积记作S1;再作第二个正方形A2B2C2A3,面积记作S2;继续作第三个正方形A3B3C3A4,面积记作S3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第6个正方形的面积S6是