题目内容
11.解方程组$\left\{\begin{array}{l}{3x-2(x+2y)=3}\\{11x+4(x+2y)=45}\end{array}\right.$.分析 方程组整理后,利用加减消元法求出解即可.
解答 解:方程组整理得:$\left\{\begin{array}{l}{x-4y=3①}\\{15x+8y=45②}\end{array}\right.$,
①×2+②得:17x=51,即x=3,
把x=3代入①得:y=0,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
6.已知直角三角形两边的长为3和4,则第三边的长为( )
| A. | 7 | B. | 5 | C. | 5或$\sqrt{7}$ | D. | 以上都不对 |
1.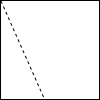 如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )
如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )
 如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )
如图,将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分,利用这两部分不能拼成的图形是( )| A. | 直角三角形 | B. | 平行四边形 | C. | 菱形 | D. | 等腰梯形 |
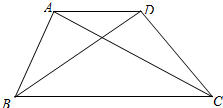 已知:如图,在梯形ABCD中,AD∥BC,CA⊥AB,cos∠ABC=$\frac{\sqrt{5}}{5}$,BC=5,AD=2.求:
已知:如图,在梯形ABCD中,AD∥BC,CA⊥AB,cos∠ABC=$\frac{\sqrt{5}}{5}$,BC=5,AD=2.求: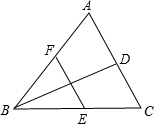 如图,点D、E、F分别是AC、BC、AB中点,且 BD是△ABC的角平分线.求证:BE=AF.
如图,点D、E、F分别是AC、BC、AB中点,且 BD是△ABC的角平分线.求证:BE=AF.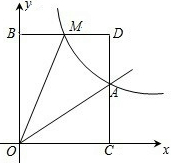 已知,如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,2).
已知,如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,2).